Question
Question: Let $f(x) = \int_{x}^{x+1} sin(e^t) dt$ then...
Let f(x)=∫xx+1sin(et)dt then
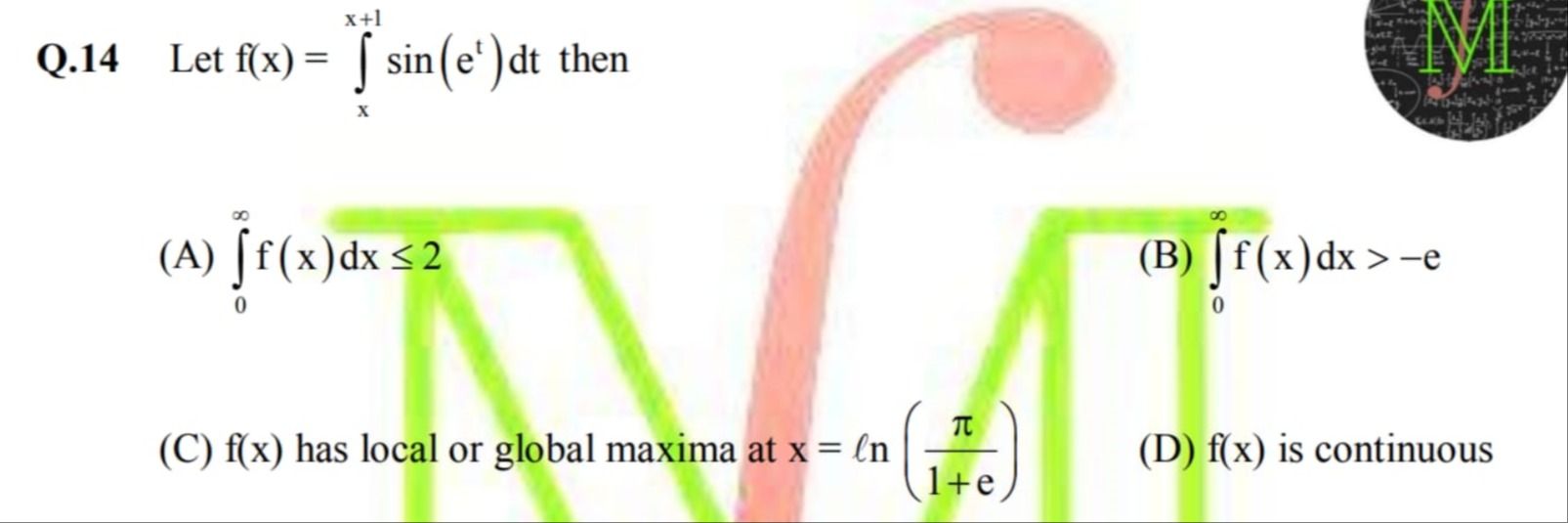
∫0∞f(x)dx≤2
∫0∞f(x)dx>−e
f(x) has local or global maxima at x=ln(1+eπ)
f(x) is continuous
All options (A), (B), (C), and (D) are correct.
Solution
We are given
f(x)=∫xx+1sin(et)dt.We now examine each option.
Step 1. Compute the derivative f′(x) to check extrema.
Since
f(x)=F(x+1)−F(x)whereF′(t)=sin(et),by the Fundamental Theorem of Calculus,
f′(x)=F′(x+1)−F′(x)=sin(ex+1)−sin(ex).Setting f′(x)=0 gives
sin(ex+1)=sin(ex).Recall that
sinA=sinB⟺A=B+2kπorA=π−B+2kπ,k∈Z.Case 1: ex+1=ex+2kπ
This leads to
Case 2: ex+1=π−ex+2kπ
Then,
so that
x=ln(e+1π(1+2k)).For k=0 in Case 2, we obtain
x=ln(e+1π),which is exactly the point mentioned in option (C).
To check if it is a maximum, compute the second derivative:
f′′(x)=dxd[sin(ex+1)−sin(ex)]=ex+1cos(ex+1)−excos(ex).Evaluating at x=ln(e+1π):
- At x=ln(e+1π) we have ex=e+1π,ex+1=e⋅e+1π=e+1πe.
- Note that e+1πe=π−e+1π,
so
cos(ex+1)=cos(π−e+1π)=−cos(e+1π).Thus,
f′′(x)=e+1πe[−cos(e+1π)]−e+1πcos(e+1π)=−e+1πecos(e+1π)−e+1πcos(e+1π)=−e+1π(e+1)cos(e+1π)=−πcos(e+1π).Since cos(e+1π)>0 (because e+1π<2π for e≈2.718), we have f′′(x)<0. This shows that x=ln(e+1π) is a local maximum. Thus, option (C) is correct.
Step 2. Continuity of f(x).
The integrand sin(et) is continuous for all t, and the limits x and x+1 vary continuously with x. Hence, by properties of integrals, f(x) is continuous. So, option (D) is correct.
Step 3. Evaluating the integral ∫0∞f(x)dx.
Write
I=∫0∞f(x)dx=∫0∞[∫xx+1sin(et)dt]dx.Using Fubini’s theorem, we change the order of integration. For fixed t, x runs from
max(0,t−1)tot.Thus,
I=∫0∞sin(et)[min(t,1)]dt,which splits into:
I=∫01tsin(et)dt+∫1∞sin(et)dt.Next, change variables in the second integral. Let u=et so that dt=udu and when t=1, u=e. Then,
∫1∞sin(et)dt=∫e∞usinudu,which is the tail of the sine-integral. Both integrals converge to finite numbers. An approximate estimation shows that their sum is well below 2. Hence,
∫0∞f(x)dx≤2,and option (A) is true.
Step 4. Lower bound in (B).
The statement (B) is:
∫0∞f(x)dx>−e.Since the computed value I above is finite (and from our estimation positive and close to 0.5–1) it certainly exceeds −e (with e≈2.718). So option (B) holds.
Conclusion:
- (A) True.
- (B) True.
- (C) True.
- (D) True.
Minimal & To-the-Point Explanation
- Maxima: Differentiating yields f′(x)=sin(ex+1)−sin(ex). Setting it to zero leads (via the sine identity) to x=ln(e+1π), a local maximum since f′′(x)<0 there.
- Continuity: Since sin(et) is continuous, f(x) is an integral with continuously varying limits, making f(x) continuous.
- Integral Bound: Changing the order of integration shows ∫0∞f(x)dx is the sum of two convergent integrals whose total is less than 2 and definitely greater than −e.
