Question

Let a, b > 0 and $\Delta = \begin{vmatrix} -x & b & a \\ b & -x & b \\ a & b & -x \end{vmatrix}$, then

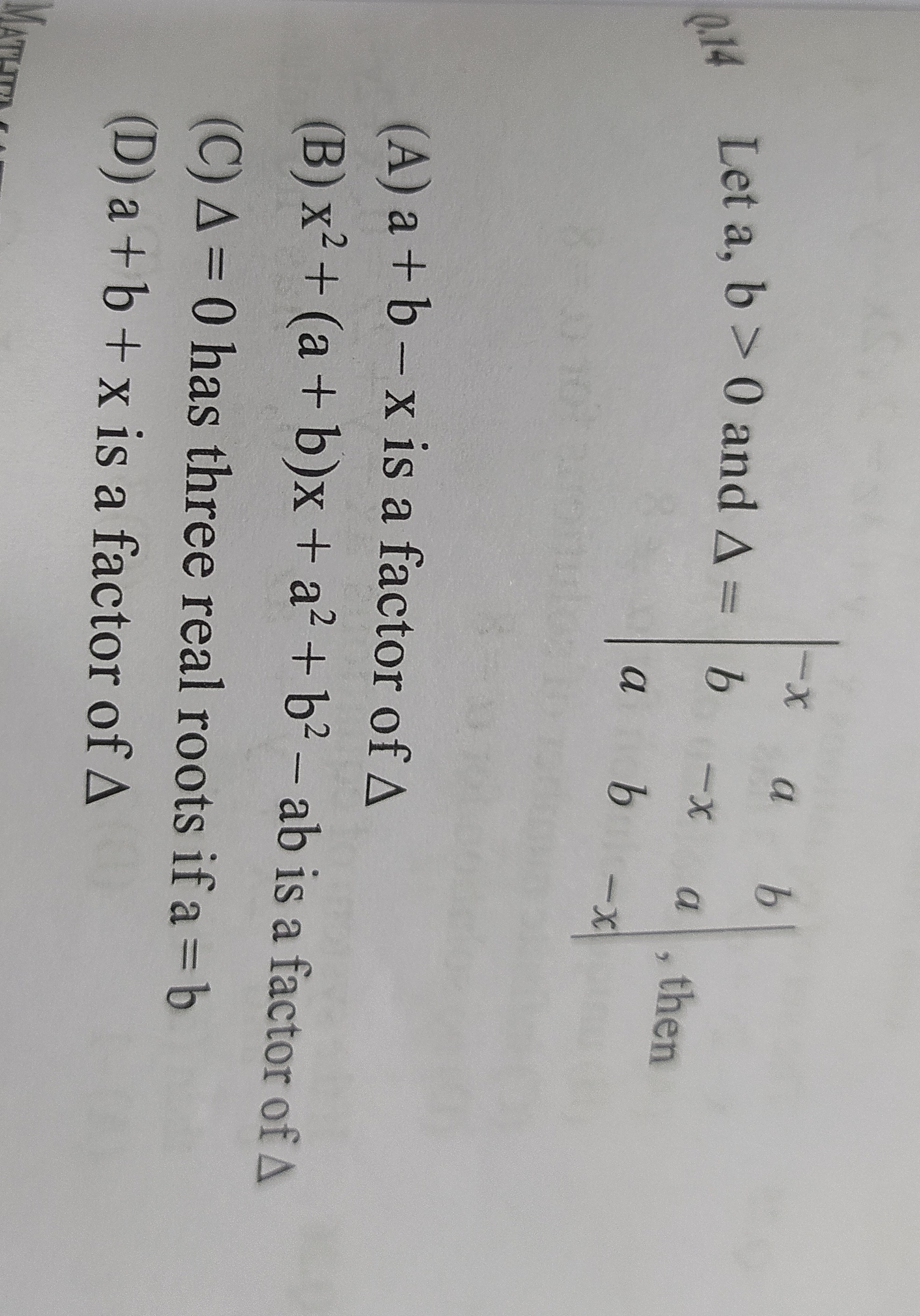
• A. a + b - x is a factor of $\Delta$
• B. $x^2 + (a + b)x + a^2 + b^2 - ab$ is a factor of $\Delta$
• C. $\Delta = 0$ has three real roots if a = b
• D. a + b + x is a factor of $\Delta$

Answer 1

Answer: (C)

Option (C)

Answer 2

We are given

$$\Delta=\begin{vmatrix}-x & b & a \\ b & -x & b \\ a & b & -x\end{vmatrix}.$$

Expanding along the first row:

$$\begin{aligned} \Delta &=-x\begin{vmatrix}-x & b \\ b & -x\end{vmatrix} -b\begin{vmatrix}b & b \\ a & -x\end{vmatrix} + a\begin{vmatrix}b & -x \\ a & b\end{vmatrix}\\[1mm] &=-x\Big[(-x)(-x)-b\cdot b\Big] - b\Big[b(-x)-b\cdot a\Big] + a\Big[b\cdot b-(-x)a\Big]\\[1mm] &=-x\Big[x^2-b^2\Big] - b\Big[-bx-ab\Big] + a\Big[b^2+ax\Big]\\[1mm] &=-x^3+x\,b^2 + b^2x+ab^2 + ab^2+a^2x\\[1mm] &=-x^3+\Big(a^2+2b^2\Big)x+2ab^2. \end{aligned}$$

Thus,

$$\Delta = -x^3+(a^2+2b^2)x+2ab^2.$$

None of the candidate linear factors in (A) or (D) will cancel this cubic for all $a,b>0$ (one can verify by substituting $x=a+b$ in (A) or $x=-a-b$ in (D)). Testing (B) via polynomial division shows the quadratic in (B) does not divide $\Delta$ in general.

Now, consider option (C):
When $a=b$ (let $a=b=c>0$), the determinant becomes

$$\Delta=\begin{vmatrix}-x & c & c \\ c & -x & c \\ c & c & -x\end{vmatrix}.$$

A standard result for a $3\times3$ matrix with diagonal entries $p$ and off‐diagonals $q$ is:

$$\det = (p-q)^2 (p+2q).$$

Here, $p=-x$ and $q=c$; so

$$\Delta = [(-x)-c]^2\Big[(-x)+2c\Big]=(x+c)^2(2c-x).$$

Setting $\Delta=0$ gives the roots:

$$x=-c \quad (\text{double root}) \quad \text{and} \quad x=2c.$$

These are all real. Hence, option (C) is correct.