Question
Question: $\int \frac{1+4^x+16^x}{1+2^x+4^x} dx$...
∫1+2x+4x1+4x+16xdx
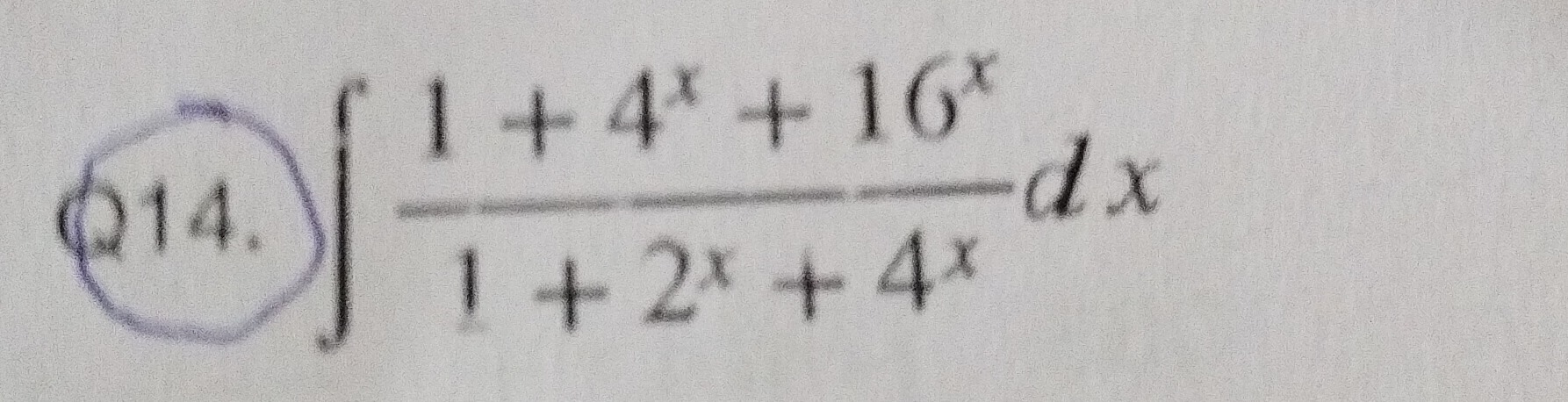
2ln24x−ln22x+x+C
Solution
The given integral is: ∫1+2x+4x1+4x+16xdx
Step 1: Simplify the integrand using substitution. Let y=2x. Then 4x=(2x)2=y2 and 16x=(2x)4=y4.
Substitute these into the integrand: 1+y+y21+y2+y4
Step 2: Apply algebraic identity to the numerator. Recall the algebraic identity for sum of powers: a4+a2+1=(a2+1)2−a2=(a2+1−a)(a2+1+a). Applying this identity with a=y, the numerator becomes: 1+y2+y4=(y2−y+1)(y2+y+1)
Step 3: Simplify the rational expression. Substitute the factored numerator back into the integrand expression: 1+y+y2(y2−y+1)(y2+y+1) Since 1+y+y2 is common to both numerator and denominator, we can cancel it out (assuming 1+y+y2=0, which is always true for real y=2x>0). The expression simplifies to: y2−y+1
Step 4: Substitute back x terms. Substitute y=2x back into the simplified expression: (2x)2−2x+1=4x−2x+1
Step 5: Integrate the simplified expression. Now, we need to integrate 4x−2x+1 with respect to x: ∫(4x−2x+1)dx Using the standard integral formula ∫axdx=lnaax+C: ∫4xdx=ln44x ∫2xdx=ln22x ∫1dx=x Combining these results: ln44x−ln22x+x+C
Step 6: Simplify the final result. We know that ln4=ln(22)=2ln2. Substitute this into the expression: 2ln24x−ln22x+x+C To combine the terms with ln2 in the denominator: 2ln24x−2⋅2x+x+C 2ln24x−2x+1+x+C
The final answer is: 2ln24x−ln22x+x+C or 2ln24x−2x+1+x+C
