Question
Question: In a parallel plate air capacitor of plate separation \(d\), a dielectric slab of thickness \(t\) is...
In a parallel plate air capacitor of plate separation d, a dielectric slab of thickness t is introduced between the plates (t<d). The capacitance becomes one-third of the original value. The dielectric constant of the slab will be
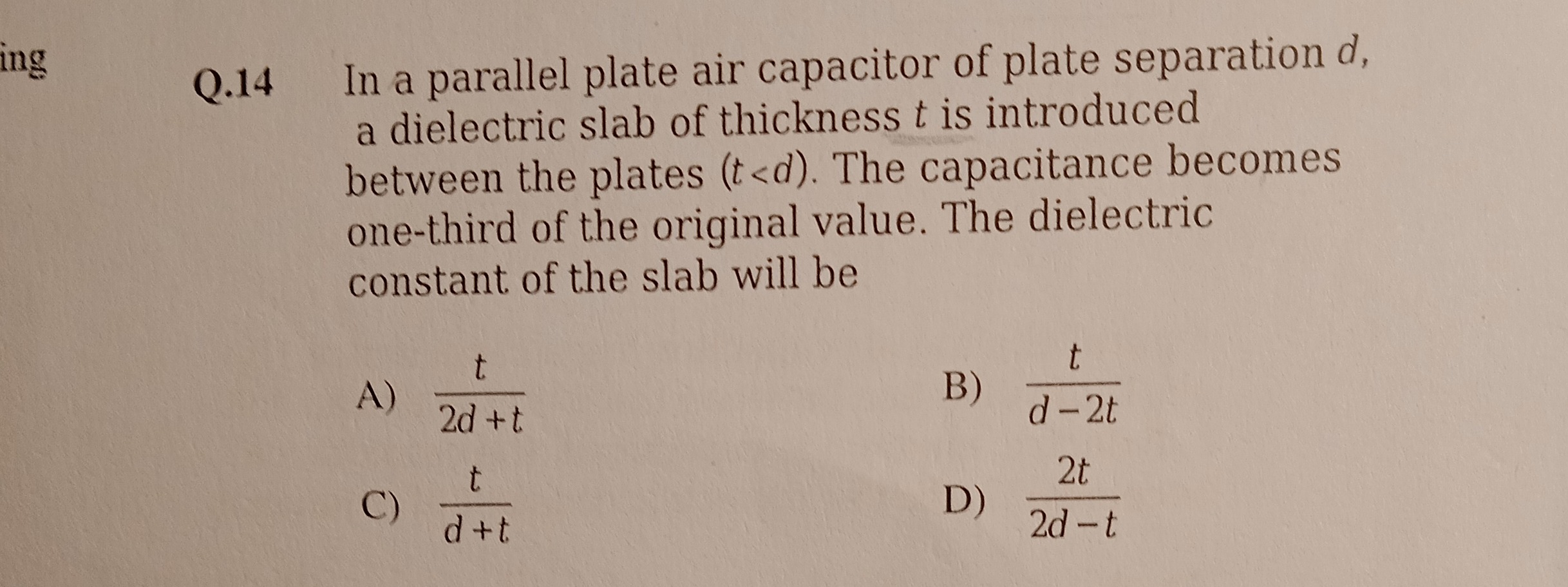
2d+tt
d−2tt
d+tt
2d−t2t
2d+tt
Solution
-
Original Capacitance: The capacitance of a parallel plate air capacitor with plate area A and separation d is given by: C0=dϵ0A
-
Capacitance with Dielectric Slab: When a dielectric slab of thickness t and dielectric constant K is introduced between the plates, the capacitor can be considered as a series combination of two air gaps (total thickness d−t) and one dielectric slab (thickness t). The effective capacitance C is given by: C=(d−t)+Ktϵ0A
-
Using the Given Condition: The problem states that the new capacitance C becomes one-third of the original capacitance C0: C=31C0
-
Substituting and Solving: Substitute the expressions for C and C0 into the equation: (d−t)+Ktϵ0A=31dϵ0A
Cancel out ϵ0A from both sides: (d−t)+Kt1=3d1
Take the reciprocal of both sides: (d−t)+Kt=3d
Isolate the term with K: Kt=3d−(d−t) Kt=3d−d+t Kt=2d+t
Solve for K: K=2d+tt
