Question

If $4x + 3y = 1, y - x - 5 = 0$ and $kx + 5y = 1$ are concurrent lines, then the value of k is

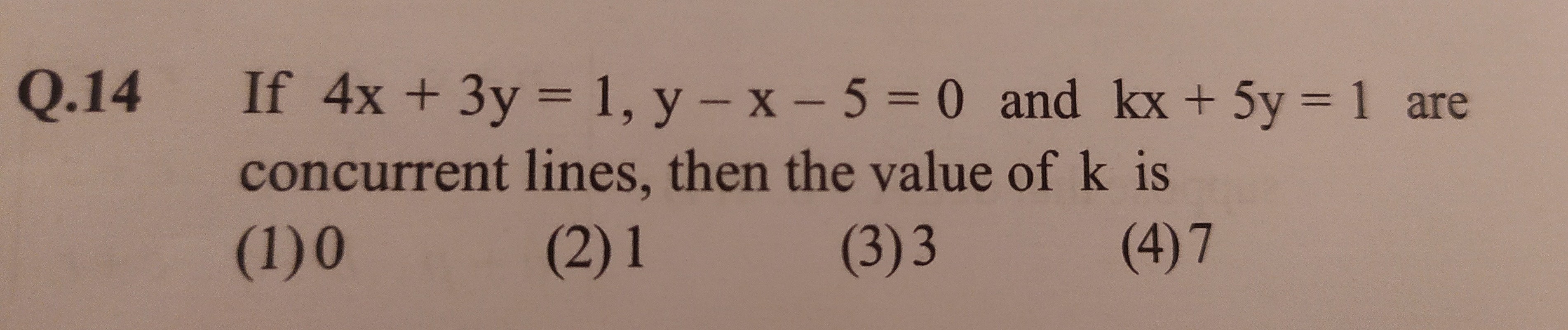
• A. 0
• B. 1
• C. 3
• D. 7

Answer 1

Answer: (D)

7

Answer 2

To find the value of $k$, we need to determine the point of intersection of the first two lines and substitute it into the third equation.

1. Solve the system of equations:

   • $4x + 3y = 1$
   • $y - x - 5 = 0 \Rightarrow y = x + 5$

2. Substitute $y$ in the first equation: $4x + 3(x + 5) = 1$ $4x + 3x + 15 = 1$ $7x = -14$ $x = -2$

3. Find $y$: $y = -2 + 5 = 3$

4. The point of intersection is $(-2, 3)$. Now substitute this point into the third equation $kx + 5y = 1$: $k(-2) + 5(3) = 1$ $-2k + 15 = 1$ $-2k = -14$ $k = 7$

Therefore, the value of $k$ is 7.