A pentagon wire mesh is formed with the help of ten resistan... | physics - equivalent resistance | SolveeIt | Solveeit

Today, August 19

Question

A pentagon wire mesh is formed with the help of ten resistance wires, each of resistance R as shown in figure. Find the equivalent resistance across ED

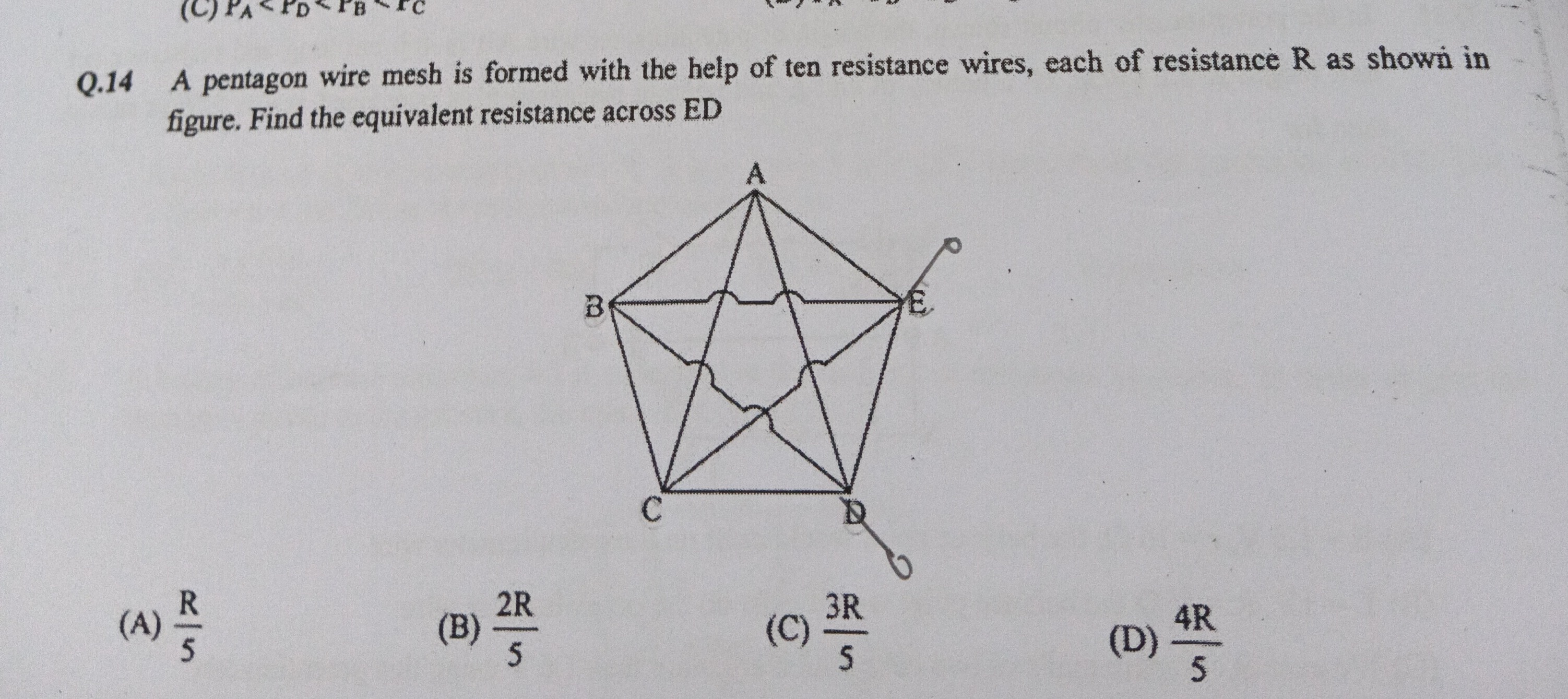
Visual representation for physics

A

$\frac{R}{5}$

B

$\frac{2R}{5}$

C

$\frac{3R}{5}$

D

$\frac{4R}{5}$

Answer

$\frac{4R}{5}$

Explanation

Solution

Assuming the question implicitly refers to a simple pentagon of 5 resistors (despite stating "ten resistance wires"), the equivalent resistance can be derived as follows:

For a simple pentagon with 5 resistors, each R, the equivalent resistance between two adjacent vertices (say E and D):

The path E-A-B-C-D has resistance 4R.

The path E-D has resistance R.

These two paths are in parallel.

So $R_{eq} = \frac{R \times 4R}{R + 4R} = \frac{4R^2}{5R} = \frac{4R}{5}$ .