Question

The number of elements in the set {$n \in \{1,2,3,...,100\} | (11)^n > (10)^n + (9)^n$} is _____.

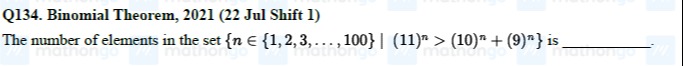
Answer 1

96

Answer 2

Solution:

1. Rewriting the Inequality:

   We have

   $11^n > 10^n + 9^n$.

   Divide both sides by $11^n$:

   $1 > \left(\frac{10}{11}\right)^n + \left(\frac{9}{11}\right)^n$.

2. Testing for the Smallest $n$:

   Check for small values of $n$:

   • For $n=1$:

     $\frac{10}{11}+\frac{9}{11}=\frac{19}{11}\approx1.727>1$.

   • For $n=2$:

     $\left(\frac{10}{11}\right)^2+\left(\frac{9}{11}\right)^2=\frac{100+81}{121}=\frac{181}{121}\approx1.495>1$.

   • For $n=4$, the sum is still greater than 1 (detailed calculation omitted here).

   • For $n=5$:

     $\left(\frac{10}{11}\right)^5+\left(\frac{9}{11}\right)^5 < 1$.

   Thus, the inequality first holds at $n=5$.

3. Counting Valid $n$:

   Valid $n$ values are from $5$ to $100$ (inclusive).

   Number of such $n$ is:

   $100 - 5 + 1 = 96$.