Question

Let a and b be two nonzero real numbers. If the coefficient of $x^5$ in the expansion of $(\frac{70}{ax^2}+\frac{ax}{27bx})^4$ is equal to the coefficient of $x^{-5}$ in the expansion of $(ax-\frac{1}{bx^2})^7$, then the value of 2b is

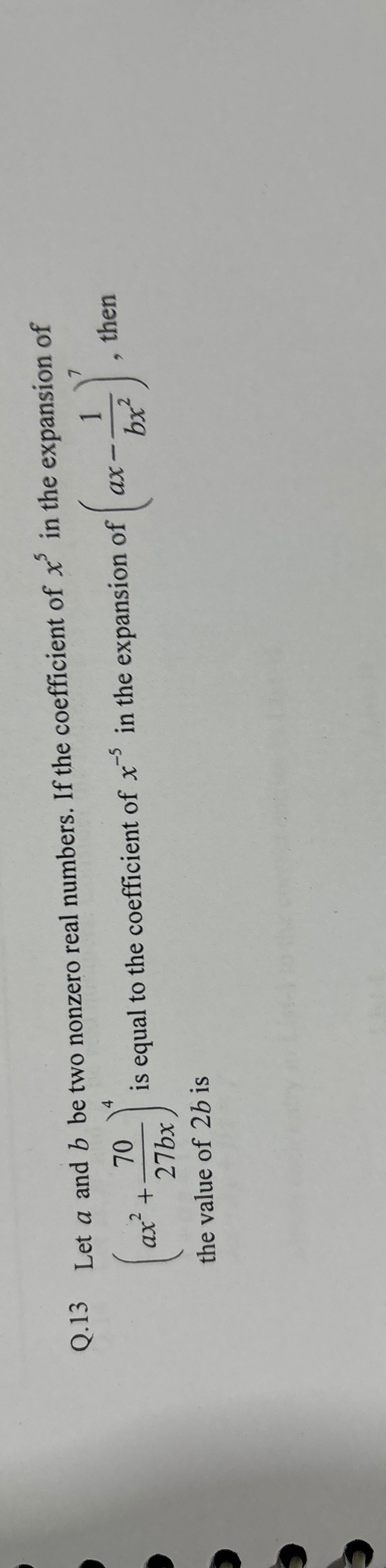
• A. 1
• B. 2
• C. 3
• D. 4

Answer 1

Answer: (C)

3

Answer 2

Solution Explanation:

1. Write the general term for the expansion of

$$\left(ax^2+\frac{70}{27bx}\right)^4:$$ $$T_{r+1} = \binom{4}{r}(ax^2)^{4-r}\left(\frac{70}{27b\,x}\right)^r.$$

The power of $x$ in $T_{r+1}$ is:

$$2(4-r)-r = 8-3r.$$

For the term in $x^5$:

$$8-3r = 5 \quad\Rightarrow\quad r=1.$$

Thus, the coefficient is:

$$\binom{4}{1}a^{3}\left(\frac{70}{27b}\right)= 4a^3\left(\frac{70}{27b}\right).$$

2. Write the general term for the expansion of

$$\left(ax-\frac{1}{bx^2}\right)^7:$$ $$T_{r+1} = \binom{7}{r}(ax)^{7-r}\left(-\frac{1}{bx^2}\right)^r.$$

The power of $x$ in $T_{r+1}$ is:

$$(7-r)-2r = 7-3r.$$

For the term in $x^{-5}$:

$$7-3r = -5 \quad\Rightarrow\quad 3r = 12 \quad\Rightarrow\quad r=4.$$

Thus, the coefficient is:

$$\binom{7}{4}a^{3}\frac{(-1)^4}{b^4} = \binom{7}{4}\frac{a^3}{b^4}.$$

Since $\binom{7}{4}=35$, this coefficient equals $\displaystyle 35\frac{a^3}{b^4}$.

3. Equate the two coefficients (ignoring the common $a^3$):

$$4\left(\frac{70}{27b}\right)=\frac{35}{b^4}.$$

This simplifies to:

$$\frac{280}{27b}=\frac{35}{b^4}.$$

Multiplying both sides by $27b^4$:

$$280b^3=35\times 27.$$

So,

$$b^3=\frac{35\times 27}{280}=\frac{945}{280}=\frac{27}{8}\quad \Rightarrow \quad b=\frac{3}{2}.$$

Therefore, $2b=3$.

Answer: $3$ (Option: 3)

Subject: Mathematics
Chapter: Binomial Theorem
Topic: Binomial Expansion

Difficulty Level: Medium
Question Type: multiple_choice