Question
Question: Four charges each equal to Q are placed at the four Q.19 corners of a square and a charge q is place...
Four charges each equal to Q are placed at the four Q.19 corners of a square and a charge q is placed at the centre of the square. If the system is in equilibrium then the value of q is
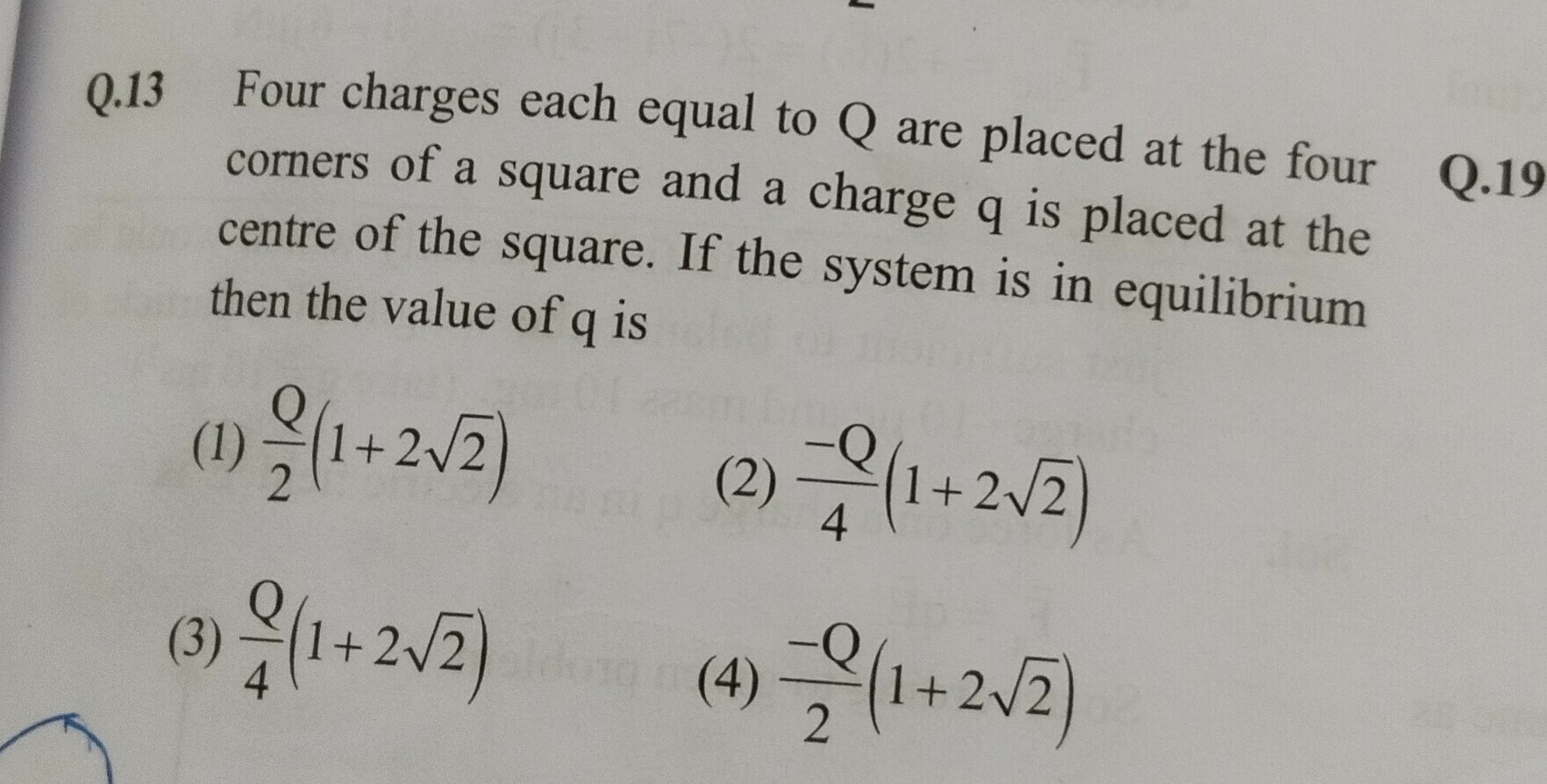
2Q(1+22)
4−Q(1+22)
4Q(1+22)
2−Q(1+22)
4−Q(1+22)
Solution
To achieve equilibrium, the net force on each charge in the system must be zero. Consider one of the corner charges (+Q). It experiences repulsive forces from the other three corner charges. The charge q at the center must exert an attractive force on this corner charge to balance the repulsive forces.
-
Forces from corner charges: Calculate the net repulsive force on a corner charge (+Q) due to the other three corner charges. This involves vector addition of the forces.
-
Force from the center charge: The force from the center charge q must counteract the net repulsive force calculated in step 1. Since the force must be attractive, q must be negative.
-
Equilibrium Condition: Set the attractive force equal to the repulsive force and solve for q. This gives q=−4Q(1+22).
