Question

Q.12 $x^2-(k+6)x+2(2k-1)$

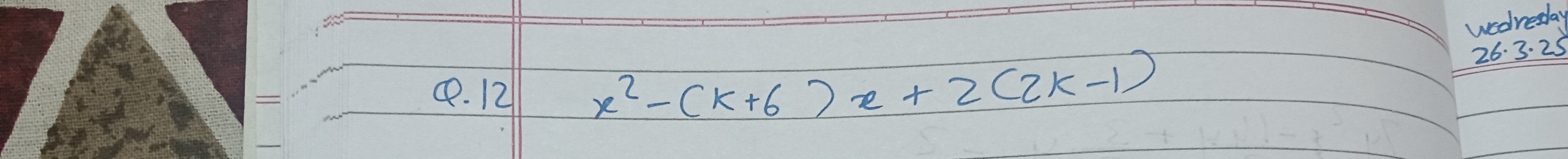
Answer 1

The quadratic $x^2-(k+6)x+2(2k-1)$ has two distinct real roots for all real numbers $k$.

Answer 2

Solution:

We are given the quadratic

$$f(x)=x^2-(k+6)x+2(2k-1).$$

To have real roots, the discriminant must be non‐negative. The discriminant $\Delta$ is

$$\Delta=(k+6)^2-4\cdot1\cdot2(2k-1).$$

Step 1: Expand and simplify the discriminant

$$\Delta=(k+6)^2-8(2k-1).$$

Expanding,

$$(k+6)^2=k^2+12k+36,$$

and

$$8(2k-1)=16k-8.$$

Thus,

$$\Delta=k^2+12k+36-16k+8=k^2-4k+44.$$

Step 2: Write in a completed square form

Complete the square for $k^2-4k+44$:

$$k^2-4k+44=(k^2-4k+4)+40=(k-2)^2+40.$$

Since $(k-2)^2\ge0$ for all real $k$, clearly

$$\Delta=(k-2)^2+40\ge40>0 \quad \text{for all real } k.$$

Thus, the quadratic has two distinct real roots for every $k\in \mathbb{R}$.

---

Explanation (minimal):

1. Write the discriminant $\Delta=(k+6)^2-8(2k-1)$.
2. Simplify it to $\Delta=(k-2)^2+40$.
3. Since $(k-2)^2\ge0$, $\Delta\ge40>0$ for all $k$.

---