Question

Let z be a complex number with |z| = 1. Then the maximum value of |z + 1| + |z² - z + 1| is

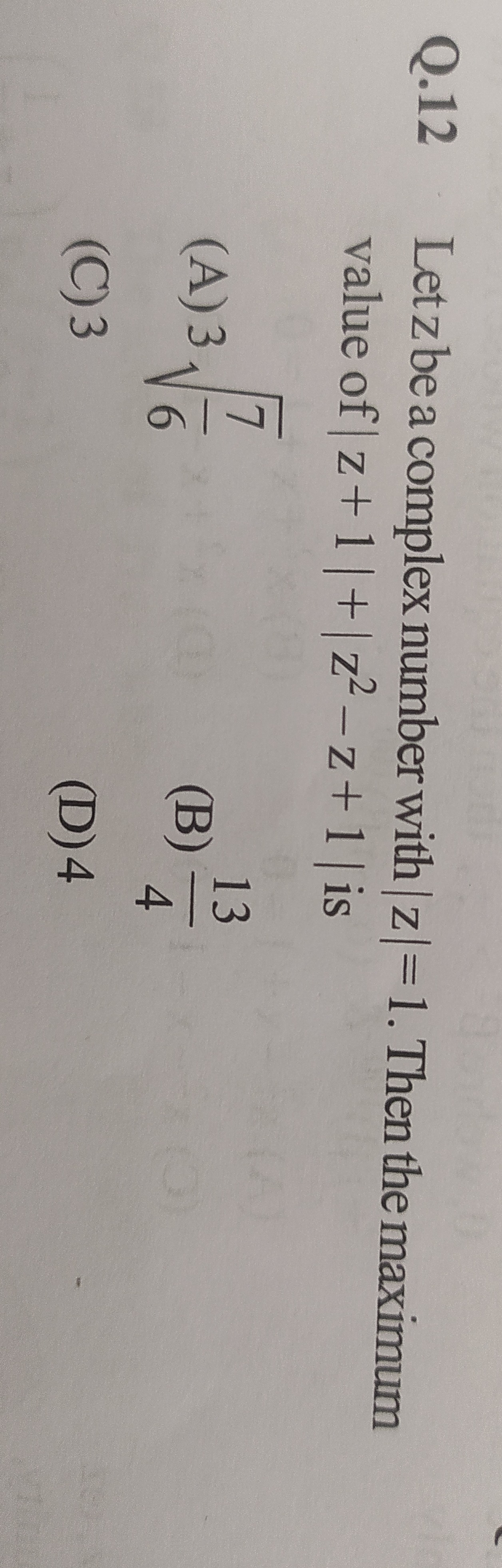
• A. $3\sqrt{\frac{7}{6}}$
• B. $\frac{13}{4}$
• C. 3
• D. 4

Answer 1

Answer: (B)

$\frac{13}{4}$

Answer 2

We are given a complex number $z$ with $|z|=1$. Let

$$z=e^{i\theta}.$$

Then,

$$|z+1| = |e^{i\theta}+1| = \sqrt{(1+\cos\theta)^2+\sin^2\theta} = \sqrt{2+2\cos\theta} = 2\cos\frac{\theta}{2}\quad (\text{when } 0\le \theta \le \pi)$$

and

$$z^2-z+1 = e^{2i\theta} - e^{i\theta} + 1.$$

Multiply and divide by $e^{-i\theta}$ (which has absolute value 1):

$$z^2-z+1 = e^{i\theta}\Bigl(e^{i\theta}+e^{-i\theta}-1\Bigr)= e^{i\theta}(2\cos\theta-1).$$

Thus,

$$|z^2-z+1| = |2\cos\theta-1|.$$

The expression to maximize is:

$$F(\theta)=2\cos\frac{\theta}{2} + |2\cos\theta-1|.$$

Set $x=\cos\theta$, so that

$$F(x)=\sqrt{2(1+x)} + |2x-1|,\quad x\in[-1,1].$$

Case 1: $x\ge \frac{1}{2}$
Here, $|2x-1|=2x-1$ so:

$$F(x)=\sqrt{2(1+x)}+(2x-1).$$

Differentiate $F(x)$ with respect to $x$:

$$F'(x)=\frac{1}{\sqrt{2(1+x)}}+2.$$

Since $F'(x)>0$ for $x\ge \frac{1}{2}$, $F(x)$ is increasing and its maximum in this region occurs at $x=1$:

$$F(1)=\sqrt{2(2)}+(2-1)=\sqrt{4}+1=2+1=3.$$

Case 2: $x<\frac{1}{2}$
Here, $|2x-1|=1-2x$, so:

$$F(x)=\sqrt{2(1+x)}+(1-2x).$$

Differentiate:

$$F'(x)=\frac{1}{\sqrt{2(1+x)}} - 2.$$

Set $F'(x)=0$:

$$\frac{1}{\sqrt{2(1+x)}} = 2 \quad \Longrightarrow \quad \sqrt{2(1+x)} = \frac{1}{2} \quad \Longrightarrow \quad 2(1+x)=\frac{1}{4}.$$

Thus,

$$1+x=\frac{1}{8}\quad\Rightarrow\quad x=-\frac{7}{8}.$$

Evaluate $F(x)$ at $x=-\frac{7}{8}$:

$$\sqrt{2\left(1- \frac{7}{8}\right)} = \sqrt{2\cdot\frac{1}{8}} = \sqrt{\frac{1}{4}}= \frac{1}{2},$$

and

$$1-2\left(-\frac{7}{8}\right)=1+\frac{7}{4}=\frac{11}{4}.$$

So,

$$F\left(-\frac{7}{8}\right)= \frac{1}{2}+\frac{11}{4} = \frac{1}{2}+\frac{11}{4} = \frac{2}{4}+\frac{11}{4} = \frac{13}{4} = 3.25.$$

Thus, the maximum value is $\frac{13}{4}$.