Question

The x-z plane separates two media A and B of refractive index $\mu_1 = 1.5$ and $\mu_2 = 2$. A ray of light-travels from A to B. Its direction in the two media, are given by unit vectors $\vec{u_1} = a\hat{i} + b\hat{j}$ and $\vec{u_2} = c\hat{i} + d\hat{j}$, then (positive y-axis medium A & -ve y-axis medium B)

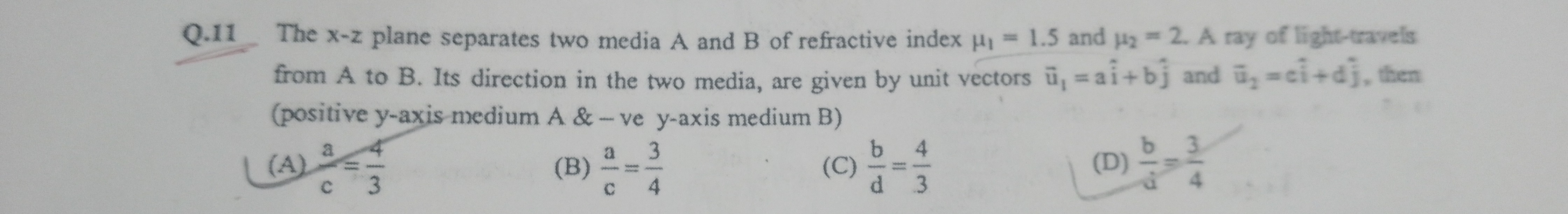
• A. $\frac{a}{c} = \frac{4}{3}$
• B. $\frac{a}{c} = \frac{3}{4}$
• C. $\frac{b}{d} = \frac{4}{3}$
• D. $\frac{b}{d} = \frac{3}{4}$

Answer 1

Answer: (A)

$\frac{a}{c} = \frac{4}{3}$

Answer 2

The tangential component of the wave vector is continuous across the interface. The wave vector is given by $\vec{k} = \frac{2\pi \mu}{\lambda_0} \vec{u}$. The interface is the x-z plane, and the normal is $\hat{j}$. The tangential component condition is $\vec{k_1} \times \hat{n} = \vec{k_2} \times \hat{n}$.

$\vec{k_1} \times \hat{j} = (\frac{2\pi \mu_1}{\lambda_0} (a\hat{i} + b\hat{j})) \times \hat{j} = \frac{2\pi \mu_1}{\lambda_0} a (\hat{i} \times \hat{j}) = \frac{2\pi \mu_1}{\lambda_0} a \hat{k}$ $\vec{k_2} \times \hat{j} = (\frac{2\pi \mu_2}{\lambda_0} (c\hat{i} + d\hat{j})) \times \hat{j} = \frac{2\pi \mu_2}{\lambda_0} c (\hat{i} \times \hat{j}) = \frac{2\pi \mu_2}{\lambda_0} c \hat{k}$

Equating these: $\frac{2\pi \mu_1}{\lambda_0} a = \frac{2\pi \mu_2}{\lambda_0} c$ $\mu_1 a = \mu_2 c$ $\frac{a}{c} = \frac{\mu_2}{\mu_1} = \frac{2}{1.5} = \frac{4}{3}$