Question

Let $|X|$ denotes the cardinal number of set $X$, and $\sum X$ denote the sum of all the elements of a finite set $X$. If

$A = \{x \in [\pi, 2\pi]|f(x) = max\{a \in \mathbb{Z} : a \leq 3 + 4 \sin x\}, f'(x) = D.N.E.\},$

$B = \{x \in [2, \infty)|f(x) = \lim_{n \to \infty} \sqrt[n]{4^x + x^{2n} + \frac{1}{x^{2n}}}, f'(x) = D.N.E.\},$

and $\sum A = k\pi$, then $k + |B|$ is equal to

Answer 1

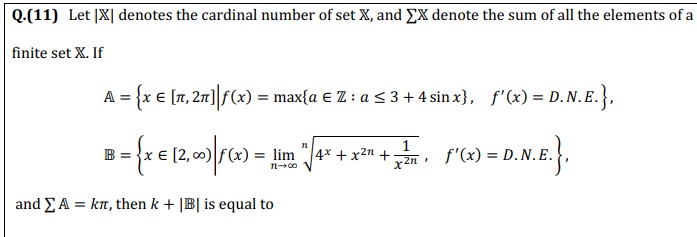
13.5

Answer 2

The problem asks for the value of $k + |B|$, where $k$ is related to the sum of elements in set $A$, and $|B|$ is the cardinal number of set $B$.

First, let's analyze set $A$: $A = \{x \in [\pi, 2\pi]|f(x) = max\{a \in \mathbb{Z} : a \leq 3 + 4 \sin x\}, f'(x) = D.N.E.\}$

The function $f(x)$ is given by $f(x) = \lfloor 3 + 4 \sin x \rfloor$. The derivative $f'(x)$ does not exist when the argument of the greatest integer function, $3 + 4 \sin x$, is an integer.

Let $3 + 4 \sin x = m$, where $m \in \mathbb{Z}$. This implies $\sin x = \frac{m-3}{4}$.

Since $-1 \leq \sin x \leq 1$, we have $-1 \leq \frac{m-3}{4} \leq 1$, which simplifies to $-4 \leq m-3 \leq 4$, or $-1 \leq m \leq 7$.

So, $m$ can be any integer from -1 to 7. The possible values of $\sin x$ are $\frac{-1}{4}, \frac{0}{4}, \frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \frac{4}{4}, \frac{5}{4}, \frac{6}{4}, \frac{7}{4}$. Wait, the denominator is 4, so the possible values are $\frac{-1-3}{4} = -1, \frac{0-3}{4} = -3/4, \frac{1-3}{4} = -1/2, \frac{2-3}{4} = -1/4, \frac{3-3}{4} = 0, \frac{4-3}{4} = 1/4, \frac{5-3}{4} = 1/2, \frac{6-3}{4} = 3/4, \frac{7-3}{4} = 1$.

We need to find the values of $x \in [\pi, 2\pi]$ such that $\sin x$ takes these values. In the interval $[\pi, 2\pi]$, $\sin x \leq 0$. So we consider $\sin x \in \{-1, -3/4, -1/2, -1/4, 0\}$.

1. $\sin x = -1$: $x = \frac{3\pi}{2}$ in $[\pi, 2\pi]$.
2. $\sin x = -3/4$: Let $\alpha = \arcsin(3/4)$, where $\alpha \in (0, \pi/2)$. The values of $x$ in $[\pi, 2\pi]$ are $\pi + \alpha$ and $2\pi - \alpha$. So $x = \pi + \arcsin(3/4)$ and $x = 2\pi - \arcsin(3/4)$.
3. $\sin x = -1/2$: The values of $x$ in $[\pi, 2\pi]$ are $\pi + \frac{\pi}{6} = \frac{7\pi}{6}$ and $2\pi - \frac{\pi}{6} = \frac{11\pi}{6}$.
4. $\sin x = -1/4$: Let $\beta = \arcsin(1/4)$, where $\beta \in (0, \pi/2)$. The values of $x$ in $[\pi, 2\pi]$ are $\pi + \beta$ and $2\pi - \beta$. So $x = \pi + \arcsin(1/4)$ and $x = 2\pi - \arcsin(1/4)$.
5. $\sin x = 0$: The values of $x$ in $[\pi, 2\pi]$ are $\pi$ and $2\pi$.

The set $A$ consists of all these distinct values: $A = \{\frac{3\pi}{2}, \pi + \arcsin(\frac{3}{4}), 2\pi - \arcsin(\frac{3}{4}), \frac{7\pi}{6}, \frac{11\pi}{6}, \pi + \arcsin(\frac{1}{4}), 2\pi - \arcsin(\frac{1}{4}), \pi, 2\pi\}$. All these 9 values are distinct and lie within the interval $[\pi, 2\pi]$.

The sum of elements in $A$, $\sum A$: $\sum A = \frac{3\pi}{2} + (\pi + \arcsin(\frac{3}{4})) + (2\pi - \arcsin(\frac{3}{4})) + \frac{7\pi}{6} + \frac{11\pi}{6} + (\pi + \arcsin(\frac{1}{4})) + (2\pi - \arcsin(\frac{1}{4})) + \pi + 2\pi$. Using the property $(\pi + \theta) + (2\pi - \theta) = 3\pi$: $(\pi + \arcsin(3/4)) + (2\pi - \arcsin(3/4)) = 3\pi$. $(\pi + \arcsin(1/4)) + (2\pi - \arcsin(1/4)) = 3\pi$. $\sum A = \frac{3\pi}{2} + 3\pi + \frac{7\pi}{6} + \frac{11\pi}{6} + 3\pi + \pi + 2\pi$. $\sum A = \frac{3\pi}{2} + 3\pi + \frac{18\pi}{6} + 3\pi + \pi + 2\pi$. $\sum A = \frac{3\pi}{2} + 3\pi + 3\pi + 3\pi + \pi + 2\pi$. $\sum A = \frac{3\pi}{2} + 12\pi = \frac{3\pi + 24\pi}{2} = \frac{27\pi}{2}$. We are given $\sum A = k\pi$, so $k\pi = \frac{27\pi}{2}$, which gives $k = \frac{27}{2}$.

Next, let's analyze set $B$: $B = \{x \in [2, \infty)|f(x) = \lim_{n \to \infty} \sqrt[n]{4^x + x^{2n} + \frac{1}{x^{2n}}}, f'(x) = D.N.E.\}$ Let $g(x) = \lim_{n \to \infty} \sqrt[n]{4^x + x^{2n} + \frac{1}{x^{2n}}}$. For $x \in [2, \infty)$, we have $x \geq 2$, so $x^2 \geq 4$. As $n \to \infty$, $x^{2n} = (x^2)^n$ grows much faster than $4^x$ and $x^{-2n} = (x^{-2})^n = (1/x^2)^n$. We can write $g(x) = \lim_{n \to \infty} \sqrt[n]{x^{2n} \left( \frac{4^x}{x^{2n}} + 1 + \frac{1}{x^{4n}} \right)} = \lim_{n \to \infty} x^2 \sqrt[n]{\frac{4^x}{x^{2n}} + 1 + \frac{1}{x^{4n}}}$. For $x \geq 2$, $\frac{4^x}{x^{2n}} = \frac{(4^{x/n})^n}{(x^2)^n} \to 0$ as $n \to \infty$ since $x^2 \geq 4$ and $4^{x/n} \to 1$. Also, $\frac{1}{x^{4n}} \to 0$ as $n \to \infty$ for $x \geq 2$. So, $g(x) = x^2 \lim_{n \to \infty} \sqrt[n]{0 + 1 + 0} = x^2 \cdot 1 = x^2$. Thus, $f(x) = x^2$ for $x \in [2, \infty)$. The derivative of $f(x) = x^2$ is $f'(x) = 2x$. The derivative $f'(x) = 2x$ exists for all $x \in [2, \infty)$. The set $B$ contains values of $x \in [2, \infty)$ where $f'(x)$ does not exist. Since $f'(x)$ exists for all $x \in [2, \infty)$, there are no such values of $x$. Therefore, set $B$ is the empty set, $B = \emptyset$. The cardinal number of set $B$ is $|B| = 0$.

We need to find $k + |B|$. $k + |B| = \frac{27}{2} + 0 = \frac{27}{2}$.

The final answer is $\frac{27}{2}$.