Question
Question: $\int \frac{x^{2023}+x^{2025}}{(1+x+x^2)(1-x+x^2)-1}dx$...
∫(1+x+x2)(1−x+x2)−1x2023+x2025dx
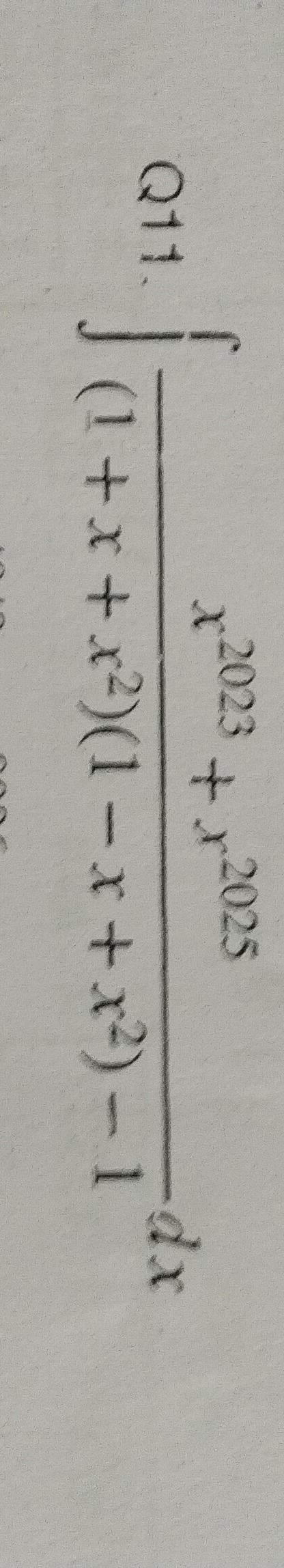
2022x2022+C
Solution
Explanation of the solution:
-
Simplify the Denominator:
The denominator is (1+x+x2)(1−x+x2)−1.
Recognize the pattern (A+B)(A−B)=A2−B2 by letting A=(1+x2) and B=x.
So, (1+x+x2)(1−x+x2)=((1+x2)+x)((1+x2)−x)
=(1+x2)2−x2
=(1+2x2+x4)−x2
=1+x2+x4
Now substitute this back into the denominator expression:
(1+x2+x4)−1=x2+x4=x2(1+x2). -
Simplify the Numerator:
The numerator is x2023+x2025.
Factor out the common term x2023:
x2023+x2025=x2023(1+x2). -
Simplify the Integrand:
Substitute the simplified numerator and denominator back into the integral:
The integrand becomes x2(1+x2)x2023(1+x2).
For x=0, the term (1+x2) can be cancelled from the numerator and denominator (since 1+x2 is never zero for real x).
Also, x2x2023=x2023−2=x2021.
Thus, the integral simplifies to ∫x2021dx. -
Evaluate the Indefinite Integral:
Apply the power rule for integration, ∫xndx=n+1xn+1+C:
∫x2021dx=2021+1x2021+1+C
=2022x2022+C.
