Question

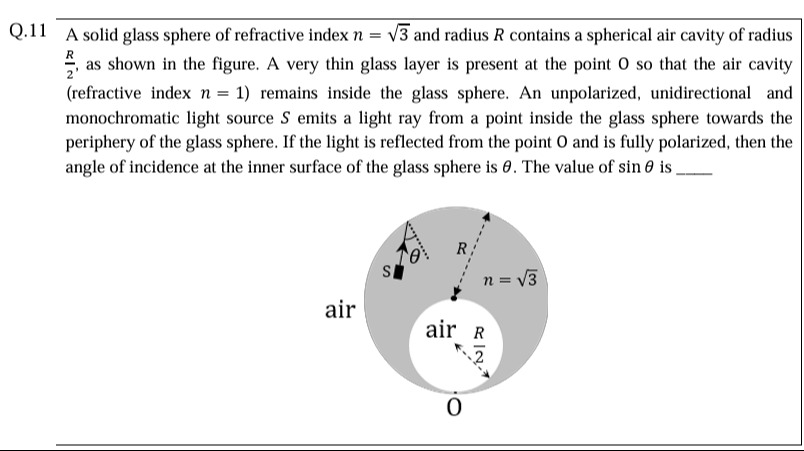
A solid glass sphere of refractive index $n = \sqrt{3}$ and radius $R$ contains a spherical air cavity of radius $\frac{R}{2}$ as shown in the figure. A very thin glass layer is present at the point $O$ so that the air cavity (refractive index $n = 1$) remains inside the glass sphere. An unpolarized, unidirectional and monochromatic light source $S$ emits a light ray from a point inside the glass sphere towards the periphery of the glass sphere. If the light is reflected from the point $O$ and is fully polarized, then the angle of incidence at the inner surface of the glass sphere is $\theta$. The value of $\sin \theta$ is ___

Answer 1

0.5

Answer 2

The problem describes a light ray traveling from a source S inside a glass sphere (refractive index $n_1 = \sqrt{3}$) and incident on a spherical air cavity (refractive index $n_2 = 1$) at point O. The light is reflected from point O, and this reflected light is stated to be fully polarized. We need to find the value of $\sin \theta$, where $\theta$ is the angle of incidence at the inner surface of the glass sphere (i.e., at point O).

According to Brewster's Law, when unpolarized light is incident on an interface between two dielectric media, the reflected light is completely polarized if the angle of incidence is equal to the Brewster's angle ($i_p$). At this angle, the reflected ray and the refracted ray are perpendicular to each other.

The formula for Brewster's angle is given by:

$$\tan i_p = \frac{n_2}{n_1}$$

where $n_1$ is the refractive index of the medium from which the light is incident, and $n_2$ is the refractive index of the medium into which the light is refracting.

In this problem:

1. The light is traveling from the glass sphere to the air cavity.
2. Refractive index of glass, $n_1 = \sqrt{3}$.
3. Refractive index of air, $n_2 = 1$.

Since the reflected light from point O is fully polarized, the angle of incidence at O must be the Brewster's angle. The problem states that the angle of incidence at O is $\theta$. Therefore, $\theta = i_p$.

Substituting the given values into Brewster's Law:

$$\tan \theta = \frac{n_{air}}{n_{glass}} = \frac{1}{\sqrt{3}}$$

We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$. Therefore, the angle of incidence $\theta = 30^\circ$.

The question asks for the value of $\sin \theta$.

$$\sin \theta = \sin 30^\circ$$ $$\sin \theta = \frac{1}{2}$$ $$\sin \theta = 0.5$$

The information about the radii $R$ and $R/2$ and the exact position of source S are not required to solve this problem, as the condition for polarization directly determines the angle of incidence.