Question

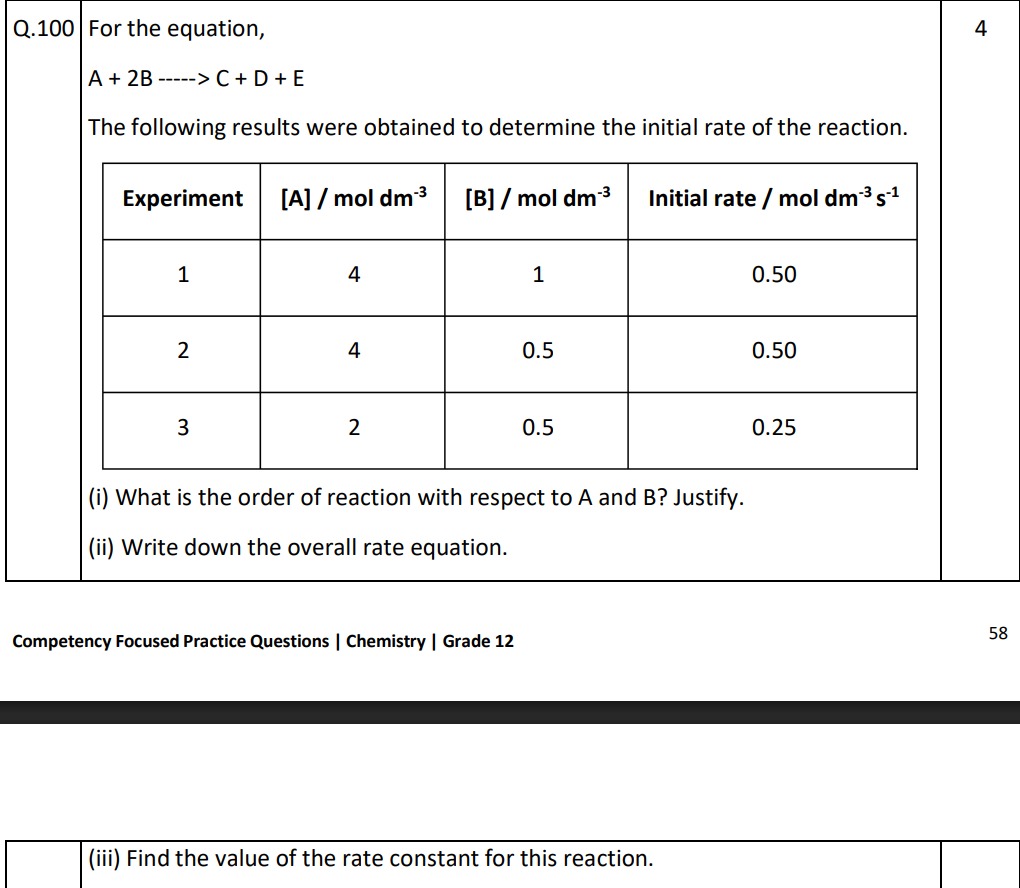
For the equation,

A + 2B -----> C + D + E

The following results were obtained to determine the initial rate of the reaction.

Experiment	[A] / mol dm⁻³	[B] / mol dm⁻³	Initial rate / mol dm⁻³ s⁻¹
1	4	1	0.50
2	4	0.5	0.50
3	2	0.5	0.25

(i) What is the order of reaction with respect to A and B? Justify.

(ii) Write down the overall rate equation.

(iii) Find the value of the rate constant for this reaction.

Answer 1

(i) The order of reaction with respect to A is 1, and with respect to B is 0.

(ii) The overall rate equation is $\text{Rate} = k[A]$.

(iii) The value of the rate constant for this reaction is $0.125 \text{ s}^{-1}$.

Answer 2

The problem requires determining the order of reaction with respect to each reactant, writing the rate equation, and calculating the rate constant using the provided experimental data.

(i) Order of reaction with respect to A and B:

• Order with respect to B: Compare Experiment 1 and Experiment 2. In Experiment 1: $[A] = 4$ mol dm⁻³, $[B] = 1$ mol dm⁻³, Initial rate $= 0.50$ mol dm⁻³ s⁻¹. In Experiment 2: $[A] = 4$ mol dm⁻³, $[B] = 0.5$ mol dm⁻³, Initial rate $= 0.50$ mol dm⁻³ s⁻¹.

  From Experiment 1 to Experiment 2, the concentration of A is kept constant, while the concentration of B is halved (from 1 to 0.5). The initial rate remains unchanged (0.50). Since the rate does not change when [B] is varied (while [A] is constant), the rate is independent of [B]. Therefore, the reaction is zero order with respect to B. Justification: Rate $\propto [B]^y$. If $[B]$ is halved and Rate remains the same, then $(1/2)^y = 1$, which implies $y = 0$.

• Order with respect to A: Compare Experiment 2 and Experiment 3. In Experiment 2: $[A] = 4$ mol dm⁻³, $[B] = 0.5$ mol dm⁻³, Initial rate $= 0.50$ mol dm⁻³ s⁻¹. In Experiment 3: $[A] = 2$ mol dm⁻³, $[B] = 0.5$ mol dm⁻³, Initial rate $= 0.25$ mol dm⁻³ s⁻¹.

  From Experiment 2 to Experiment 3, the concentration of B is kept constant, while the concentration of A is halved (from 4 to 2). The initial rate is also halved (from 0.50 to 0.25). Since the rate is halved when [A] is halved (while [B] is constant), the rate is directly proportional to [A]. Therefore, the reaction is first order with respect to A. Justification: Rate $\propto [A]^x$. If $[A]$ is halved and Rate is halved, then $(1/2)^x = 1/2$, which implies $x = 1$.

(ii) Overall rate equation:

The general rate law is given by: $\text{Rate} = k[A]^x[B]^y$ Substituting the determined orders $x=1$ and $y=0$: $\text{Rate} = k[A]^1[B]^0$ Since $[B]^0 = 1$, the overall rate equation simplifies to: $\text{Rate} = k[A]$

(iii) Value of the rate constant for this reaction:

We can use any of the experiments and the derived rate equation $\text{Rate} = k[A]$ to calculate the rate constant $k$. Let's use Experiment 1 data: Initial rate $= 0.50$ mol dm⁻³ s⁻¹ $[A] = 4$ mol dm⁻³

Substitute these values into the rate equation: $0.50 \text{ mol dm}^{-3} \text{ s}^{-1} = k \times (4 \text{ mol dm}^{-3})$ Now, solve for $k$: $k = \frac{0.50 \text{ mol dm}^{-3} \text{ s}^{-1}}{4 \text{ mol dm}^{-3}}$ $k = 0.125 \text{ s}^{-1}$

The value of the rate constant is $0.125 \text{ s}^{-1}$.

---

Explanation of the solution:

(i) Order with respect to B: Comparing Experiment 1 and 2, [A] is constant, [B] is halved, and the rate remains constant. This implies the rate is independent of [B], hence the order with respect to B is 0.
Order with respect to A: Comparing Experiment 2 and 3, [B] is constant, [A] is halved, and the rate is halved. This implies the rate is directly proportional to [A], hence the order with respect to A is 1.

(ii) Overall Rate Equation: Based on the orders determined, the rate equation is $\text{Rate} = k[A]^1[B]^0$, which simplifies to $\text{Rate} = k[A]$.

(iii) Rate Constant (k): Using data from Experiment 1 (Rate = 0.50 mol dm⁻³ s⁻¹, [A] = 4 mol dm⁻³), substitute into the rate equation: $0.50 = k \times 4$. Solving for k gives $k = 0.125 \text{ s}^{-1}$.