Question
Question: The number of solutions of the equation $\left(\frac{9}{x} - \frac{9}{\sqrt{x}} + 2\right)\left(\fra...
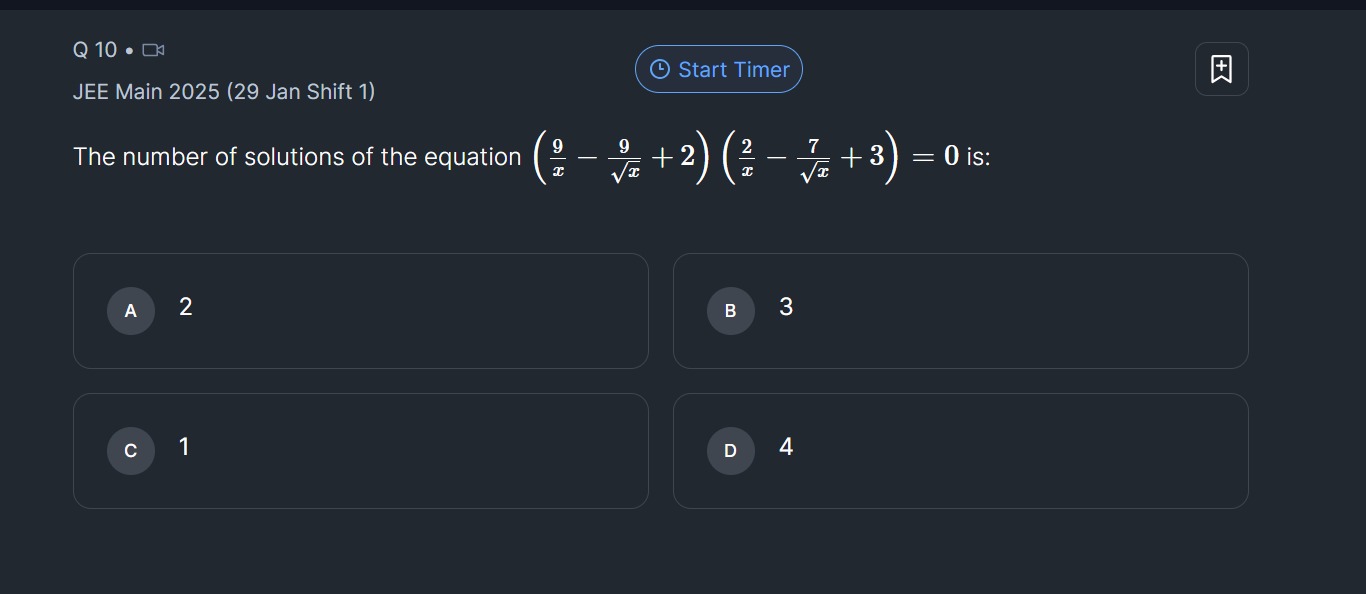
The number of solutions of the equation (x9−x9+2)(x2−x7+3)=0 is:
A
2
B
3
C
1
D
4
Answer
4
Explanation
Solution
Let y=x1. The equation transforms to (9y2−9y+2)(2y2−7y+3)=0. The condition x>0 implies y>0. Solving 9y2−9y+2=0 yields y=31,32. Solving 2y2−7y+3=0 yields y=21,3. All four y values are positive. Each positive y corresponds to a unique positive x=1/y2. Thus, there are 4 distinct solutions.
