Question

If p, q, r, s are in A.P. and

$f(x) = \begin{vmatrix} p + sinx & q + sinx & p-r + sin x \\ q + sinx & r + sinx & -1 + sinx \\ r + sinx & s + sinx & s-q + sinx \end{vmatrix}$ such $\int_{0}^{2} f(x)dx=-4$ then the common difference of the A.P. can be:

• A.
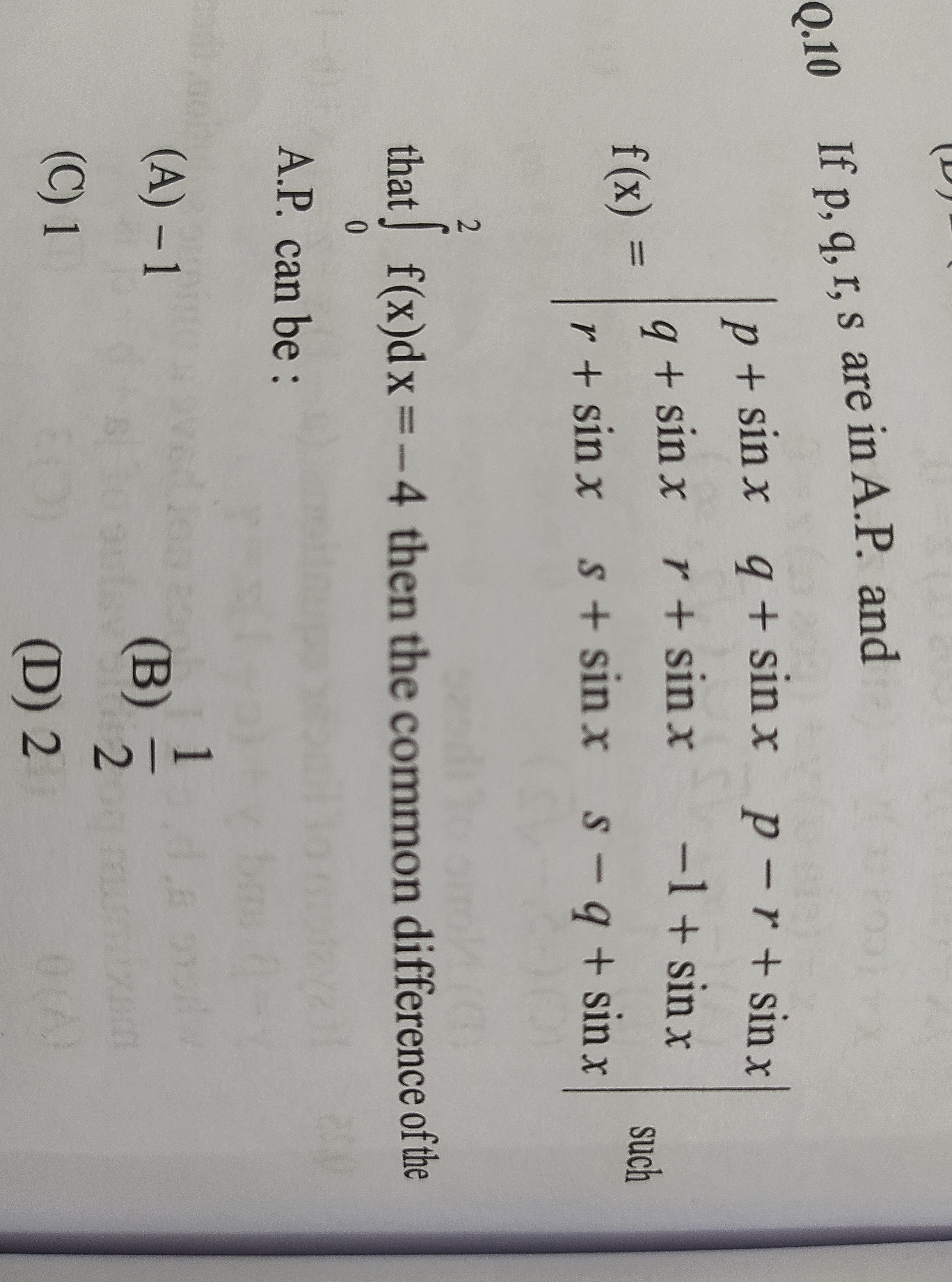
  • 1
• B. $\frac{1}{2}$
• C. 1
• D. 2

Answer 1

Answer: (A), (C)

The common difference can be -1 or 1.

Answer 2

We are given that

$$f(x)=\begin{vmatrix} p+\sin x & q+\sin x & p-r+\sin x\\[1mm] q+\sin x & r+\sin x & -1+\sin x\\[1mm] r+\sin x & s+\sin x & s-q+\sin x \end{vmatrix}$$

with $p,q,r,s$ in A.P. Write

$$q=p+d,\quad r=p+2d,\quad s=p+3d.$$

Thus the matrix becomes

$$\begin{array}{ccc} p+\sin x & p+d+\sin x & \;p-(p+2d)+\sin x \;=\; \sin x-2d\\[1mm] p+d+\sin x & p+2d+\sin x & -1+\sin x\\[1mm] p+2d+\sin x & p+3d+\sin x & (p+3d)-(p+d)+\sin x = \sin x+2d \end{array}.$$

Step 1. Subtract the first row from the other two:

Let

$$\begin{array}{rcl} R_1 & = & [\,p+\sin x,\;p+d+\sin x,\;\sin x-2d\,],\\[1mm] R_2 & \to & R_2-R_1: \quad [d,\; d,\; (-1+\sin x)-(\sin x-2d)=2d-1],\\[1mm] R_3 & \to & R_3-R_1: \quad [2d,\; 2d,\; (\sin x+2d)-(\sin x-2d)=4d]. \end{array}$$

So the new matrix (which we call $M$) is

$$M=\begin{pmatrix} p+\sin x & p+d+\sin x & \sin x-2d\\[1mm] d & d & 2d-1\\[1mm] 2d & 2d & 4d \end{pmatrix}.$$

Step 2. Remove $p$ from the 2nd column:

Subtract column 1 from column 2 ($C_2 \to C_2-C_1$). Then

$$\begin{array}{rcl} \text{Row 1: } & (p+d+\sin x)-(p+\sin x) &= d,\\[1mm] \text{Rows 2,3: } & d-d &= 0,\quad 2d-2d=0. \end{array}$$

Thus the matrix becomes

$$M=\begin{pmatrix} p+\sin x & d & \sin x-2d\\[1mm] d & 0 & 2d-1\\[1mm] 2d & 0 & 4d \end{pmatrix}.$$

Step 3. Expand the determinant along the 2nd column:

Since the 2nd column is $[d,\,0,\,0]^T$ we have

$$f(x)=(-1)^{1+2}\,d\cdot\begin{vmatrix} d & 2d-1\\[1mm] 2d & 4d\end{vmatrix} = -d\Bigl[d(4d)-2d(2d-1)\Bigr].$$

Compute the $2\times2$ determinant:

$$d(4d)-2d(2d-1)= 4d^2- \;4d^2+2d=2d.$$

Thus

$$f(x) = -d\,(2d)= -2d^2.$$

Notice that the resulting $f(x)$ is independent of $x$ (and therefore independent of $\sin x$) and also independent of $p$.

Step 4. Use the given integral:

$$\int_{0}^{2} f(x)\,dx = \int_0^2 (-2d^2)\,dx = -2d^2\cdot 2=-4d^2.$$

We are told this equals $-4$. Therefore:

$$-4d^2=-4\quad\Longrightarrow\quad d^2=1.$$

So

$$d=\pm 1.$$

Among the given options
(A) $-1$ (B) $\tfrac{1}{2}$ (C) $1$ (D) $2$
both $-1$ and $1$ satisfy the equation.