Question

Q.10 $\Delta$ G° of the cell reaction $AgCl(s) + \frac{1}{2}H_2(g) \rightarrow Ag(s) + H^+ + Cl^-$ is -21.52 KJ $\Delta$ G° of $2AgCl(s) + H_2(g) \rightarrow 2Ag(s) + 2H^+ + 2Cl^-$ is:

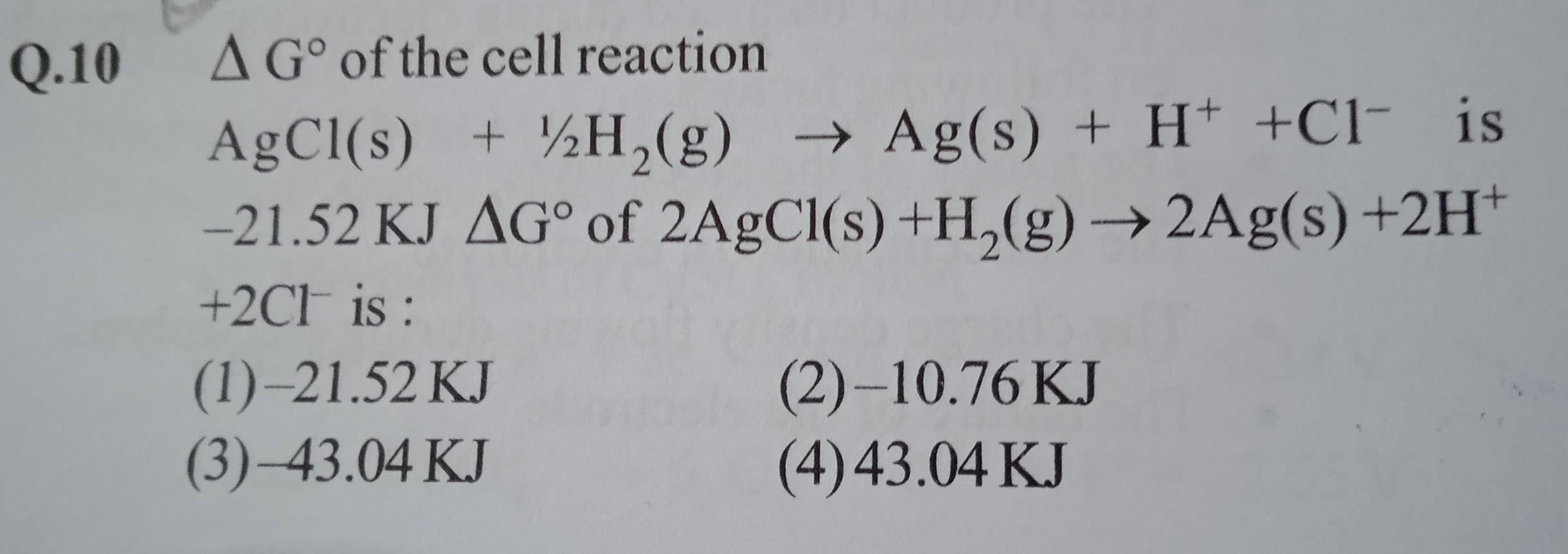
• A. -21.52 KJ
• B. -43.04 KJ
• C. -10.76 KJ
• D. 43.04 KJ

Answer 1

Answer: (B)

-43.04 KJ

Answer 2

The Gibbs free energy change ($\Delta G^\circ$) is an extensive property, meaning its value depends on the amount of substance involved in the reaction. If a chemical reaction is multiplied by a stoichiometric factor, the corresponding $\Delta G^\circ$ value is also multiplied by the same factor.

The given reaction is:

$AgCl(s) + \frac{1}{2}H_2(g) \rightarrow Ag(s) + H^+ + Cl^-$

For this reaction, $\Delta G^\circ_1 = -21.52$ KJ.

The reaction for which $\Delta G^\circ$ is to be found is:

$2AgCl(s) + H_2(g) \rightarrow 2Ag(s) + 2H^+ + 2Cl^-$

Comparing the two reactions, it is clear that the second reaction is exactly twice the first reaction. If we multiply the first reaction by 2:

$2 \times (AgCl(s) + \frac{1}{2}H_2(g) \rightarrow Ag(s) + H^+ + Cl^-)$

This gives:

$2AgCl(s) + H_2(g) \rightarrow 2Ag(s) + 2H^+ + 2Cl^-$

Since the second reaction is obtained by multiplying the first reaction by a factor of 2, the $\Delta G^\circ$ for the second reaction ($\Delta G^\circ_2$) will be twice the $\Delta G^\circ$ of the first reaction ($\Delta G^\circ_1$).

$\Delta G^\circ_2 = 2 \times \Delta G^\circ_1$

$\Delta G^\circ_2 = 2 \times (-21.52 \text{ KJ})$

$\Delta G^\circ_2 = -43.04 \text{ KJ}$