Question

Q.1 $Zn | Zn^{2+}_{(ag)} || Cu^{2+}_{(ag)} | Cu$ Eº for the cell is 1.10 V at 25°C. The equilibrium constant for the cell reaction is of the order of

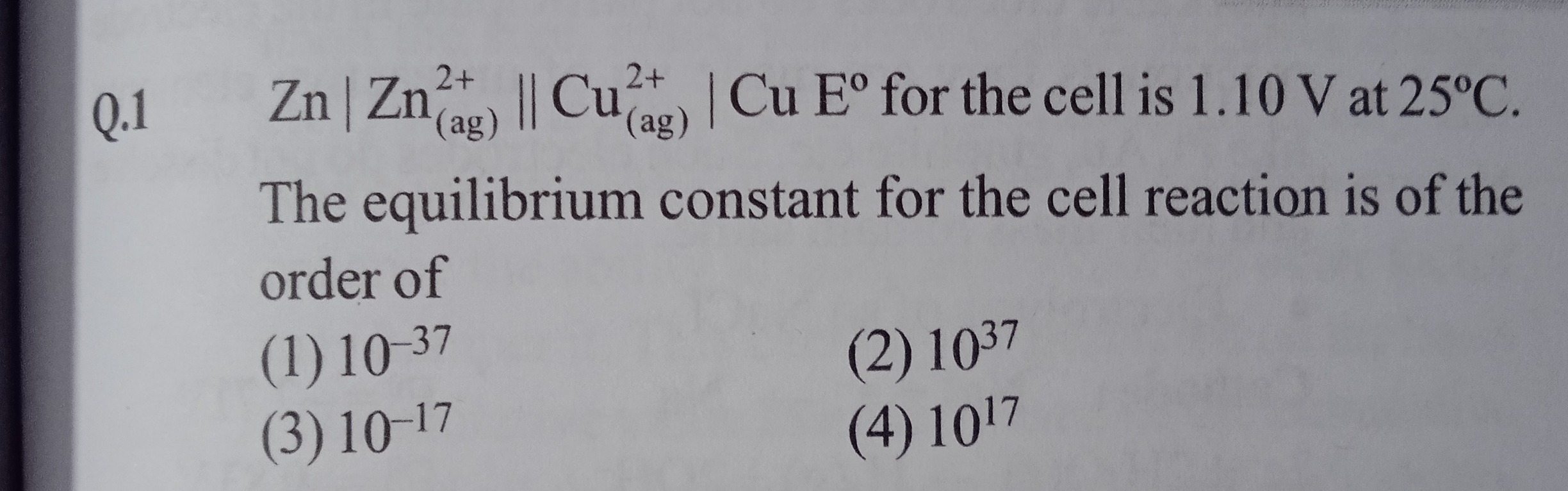
• A. $10^{-37}$
• B. $10^{37}$
• C. $10^{-17}$
• D. $10^{17}$

Answer 1

Answer: (B)

$10^{37}$

Answer 2

The electrochemical cell given is $Zn | Zn^{2+}_{(ag)} || Cu^{2+}_{(ag)} | Cu$. The standard cell potential ($E^\circ_{cell}$) is 1.10 V at 25°C.

The cell reaction can be written as:

Anode (oxidation): $Zn(s) \rightarrow Zn^{2+}(aq) + 2e^-$

Cathode (reduction): $Cu^{2+}(aq) + 2e^- \rightarrow Cu(s)$

Overall cell reaction: $Zn(s) + Cu^{2+}(aq) \rightleftharpoons Zn^{2+}(aq) + Cu(s)$

From the balanced cell reaction, the number of electrons transferred (n) is 2.

The relationship between the standard cell potential ($E^\circ_{cell}$) and the equilibrium constant (K) at 25°C is given by the formula: $\log_{10} K = \frac{nE^\circ_{cell}}{0.0592 \, V}$

Given: $E^\circ_{cell} = 1.10 \, V$ $n = 2$

Substitute these values into the formula: $\log_{10} K = \frac{2 \times 1.10}{0.0592}$ $\log_{10} K = \frac{2.20}{0.0592}$

Now, perform the division: $\log_{10} K \approx 37.16$

To find K, we take the antilog: $K = 10^{37.16}$

The question asks for the order of the equilibrium constant. Since $K = 10^{37.16}$, its order of magnitude is $10^{37}$.

Comparing this with the given options:

(1) $10^{-37}$

(2) $10^{37}$

(3) $10^{-17}$

(4) $10^{17}$

The calculated order matches option (2).