Question

Two cities $X$ and $Y$ are connected by a regular bus service with a bus leaving in either direction every $T$ min. A girl is driving scooty with a speed of 60 km/h in the direction $X$ to $Y$ notices that a bus goes past her every 30 minutes in the direction of her motion, and every 10 minutes in the opposite direction. Choose the correct option for the period $T$ of the bus service and the speed (assumed constant) of the buses.

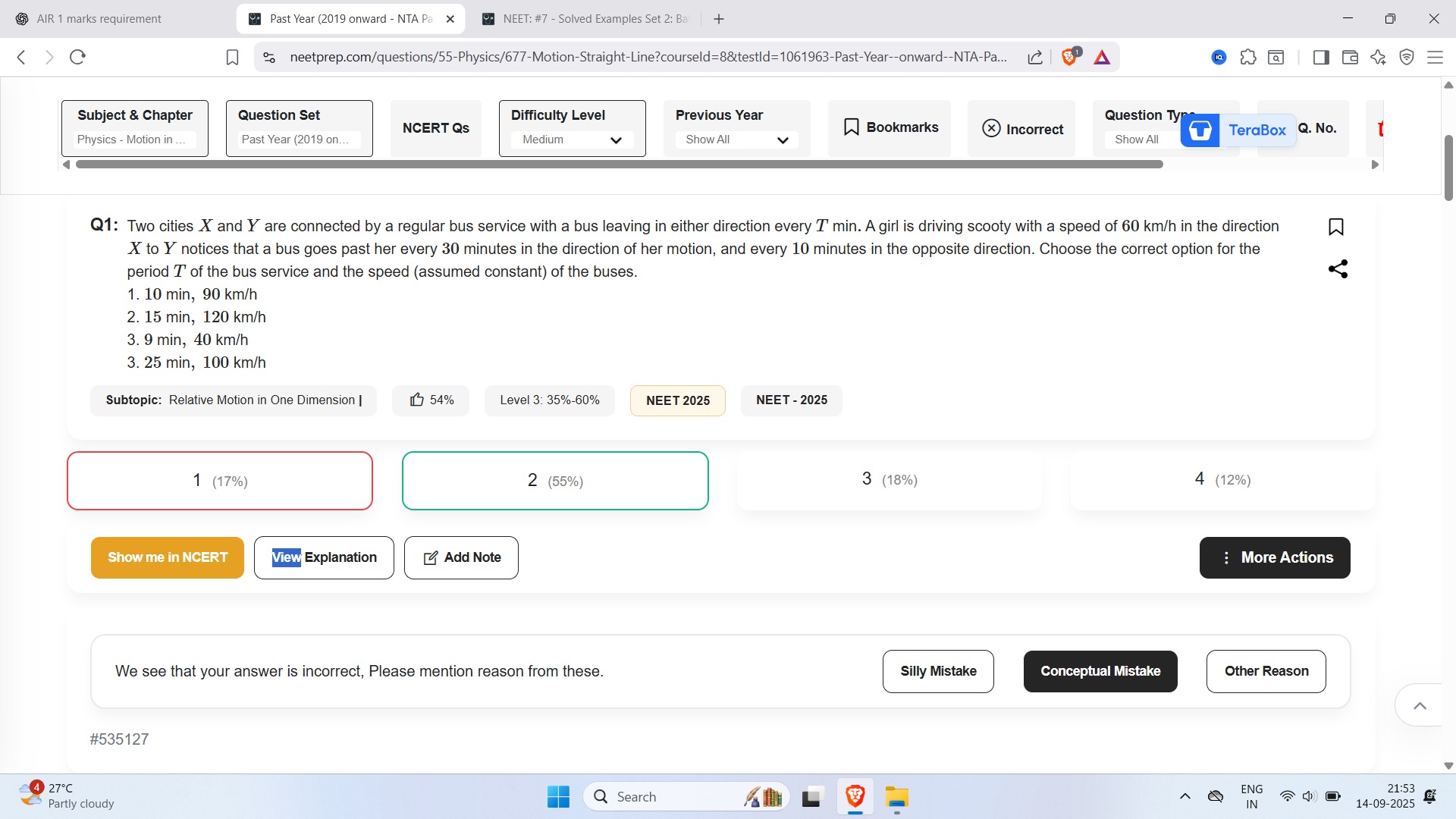
• A. 10 min, 90 km/h
• B. 15 min, 120 km/h
• C. 9 min, 40 km/h
• D. 25 min, 100 km/h

Answer 1

Answer: (B)

15 min, 120 km/h

Answer 2

Let $v_g$ be the speed of the girl's scooty and $v_b$ be the speed of the buses. Let $T$ be the time interval between consecutive buses leaving in one direction (in minutes). Given $v_g = 60$ km/h.

We need to convert units to be consistent. Let's use km/h for speeds and hours for time. $v_g = 60$ km/h. Let $T_{hr}$ be the period $T$ in hours, so $T_{hr} = T/60$.

The distance between two consecutive buses moving in the same direction is $d = v_b \times T_{hr}$.

Case 1: Buses moving in the same direction as the girl. The girl is moving at $v_g$ and buses are moving at $v_b$. The problem states "a bus goes past her", implying the bus is overtaking her, so $v_b > v_g$. The relative speed at which the girl encounters these buses is $v_{rel,1} = v_b - v_g$. The time interval between buses passing her in this direction is given as 30 minutes, which is $0.5$ hours. So, $0.5 = \frac{d}{v_b - v_g} = \frac{v_b T_{hr}}{v_b - v_g}$. $0.5 (v_b - 60) = v_b T_{hr}$ (Equation 1)

Case 2: Buses moving in the opposite direction to the girl. The girl is moving at $v_g$ and buses are moving at $v_b$ in the opposite direction. Their relative speed is $v_{rel,2} = v_b + v_g$. The time interval between buses passing her in this direction is given as 10 minutes, which is $1/6$ hours. So, $\frac{1}{6} = \frac{d}{v_b + v_g} = \frac{v_b T_{hr}}{v_b + v_g}$. $\frac{1}{6} (v_b + 60) = v_b T_{hr}$ (Equation 2)

Now we have a system of two equations:

1. $0.5 v_b - 30 = v_b T_{hr}$
2. $\frac{v_b}{6} + 10 = v_b T_{hr}$

Equating the right-hand sides: $0.5 v_b - 30 = \frac{v_b}{6} + 10$ $0.5 v_b - \frac{v_b}{6} = 10 + 30$ $(\frac{1}{2} - \frac{1}{6}) v_b = 40$ $(\frac{3}{6} - \frac{1}{6}) v_b = 40$ $\frac{2}{6} v_b = 40$ $\frac{1}{3} v_b = 40$ $v_b = 120$ km/h.

Now, substitute $v_b = 120$ km/h into either equation to find $v_b T_{hr}$. Using Equation 2: $v_b T_{hr} = \frac{120}{6} + 10 = 20 + 10 = 30$. So, $v_b T_{hr} = 30$. Since $v_b = 120$ km/h, we have $120 \times T_{hr} = 30$. $T_{hr} = \frac{30}{120} = \frac{1}{4}$ hours.

The question asks for the period $T$ in minutes. $T = T_{hr} \times 60 = \frac{1}{4} \times 60 = 15$ minutes.

Thus, the speed of the buses is 120 km/h and the period of the bus service is 15 minutes.