Solveeit Logo
Login

Question

Question: The values of $\frac{1}{1+x^{m-n}+x^{m-p}}+\frac{1}{1+x^{n-m}+x^{n-p}}+\frac{1}{1+x^{p-m}+x^{p-n}}$...

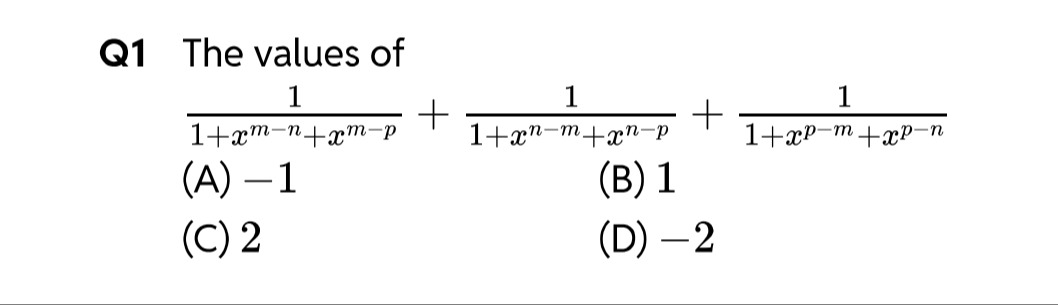
The values of 11+xm−n+xm−p+11+xn−m+xn−p+11+xp−m+xp−n\frac{1}{1+x^{m-n}+x^{m-p}}+\frac{1}{1+x^{n-m}+x^{n-p}}+\frac{1}{1+x^{p-m}+x^{p-n}}

A

-1

B

1

C

2

D

-2

Answer

1

Explanation

Solution

The problem asks us to simplify the given expression: E=11+xm−n+xm−p+11+xn−m+xn−p+11+xp−m+xp−nE = \frac{1}{1+x^{m-n}+x^{m-p}}+\frac{1}{1+x^{n-m}+x^{n-p}}+\frac{1}{1+x^{p-m}+x^{p-n}}

We will simplify each term by multiplying its numerator and denominator by a suitable factor. The goal is to make the denominators of all three terms identical.

Step 1: Simplify the first term Consider the first term: 11+xm−n+xm−p\frac{1}{1+x^{m-n}+x^{m-p}} We can rewrite the exponents using xa−b=xaxbx^{a-b} = \frac{x^a}{x^b}. So, xm−n=xmxnx^{m-n} = \frac{x^m}{x^n} and xm−p=xmxpx^{m-p} = \frac{x^m}{x^p}. The term becomes: 11+xmxn+xmxp\frac{1}{1+\frac{x^m}{x^n}+\frac{x^m}{x^p}} To get a common denominator in the denominator, we can multiply the numerator and denominator of the entire fraction by x−mx^{-m} (or 1xm\frac{1}{x^m}). 11+xm−n+xm−p=1⋅x−m(1+xm−n+xm−p)⋅x−m\frac{1}{1+x^{m-n}+x^{m-p}} = \frac{1 \cdot x^{-m}}{(1+x^{m-n}+x^{m-p}) \cdot x^{-m}} =x−mx−m⋅1+x−m⋅xm−n+x−m⋅xm−p= \frac{x^{-m}}{x^{-m} \cdot 1 + x^{-m} \cdot x^{m-n} + x^{-m} \cdot x^{m-p}} Using the rule xa⋅xb=xa+bx^a \cdot x^b = x^{a+b}: =x−mx−m+x−m+m−n+x−m+m−p= \frac{x^{-m}}{x^{-m} + x^{-m+m-n} + x^{-m+m-p}} =x−mx−m+x−n+x−p(Term 1)= \frac{x^{-m}}{x^{-m} + x^{-n} + x^{-p}} \quad \text{(Term 1)}

Step 2: Simplify the second term Consider the second term: 11+xn−m+xn−p\frac{1}{1+x^{n-m}+x^{n-p}} Similarly, multiply the numerator and denominator by x−nx^{-n}: 11+xn−m+xn−p=1⋅x−n(1+xn−m+xn−p)⋅x−n\frac{1}{1+x^{n-m}+x^{n-p}} = \frac{1 \cdot x^{-n}}{(1+x^{n-m}+x^{n-p}) \cdot x^{-n}} =x−nx−n⋅1+x−n⋅xn−m+x−n⋅xn−p= \frac{x^{-n}}{x^{-n} \cdot 1 + x^{-n} \cdot x^{n-m} + x^{-n} \cdot x^{n-p}} =x−nx−n+x−n+n−m+x−n+n−p= \frac{x^{-n}}{x^{-n} + x^{-n+n-m} + x^{-n+n-p}} =x−nx−n+x−m+x−p(Term 2)= \frac{x^{-n}}{x^{-n} + x^{-m} + x^{-p}} \quad \text{(Term 2)}

Step 3: Simplify the third term Consider the third term: 11+xp−m+xp−n\frac{1}{1+x^{p-m}+x^{p-n}} Multiply the numerator and denominator by x−px^{-p}: 11+xp−m+xp−n=1⋅x−p(1+xp−m+xp−n)⋅x−p\frac{1}{1+x^{p-m}+x^{p-n}} = \frac{1 \cdot x^{-p}}{(1+x^{p-m}+x^{p-n}) \cdot x^{-p}} =x−px−p⋅1+x−p⋅xp−m+x−p⋅xp−n= \frac{x^{-p}}{x^{-p} \cdot 1 + x^{-p} \cdot x^{p-m} + x^{-p} \cdot x^{p-n}} =x−px−p+x−p+p−m+x−p+p−n= \frac{x^{-p}}{x^{-p} + x^{-p+p-m} + x^{-p+p-n}} =x−px−p+x−m+x−n(Term 3)= \frac{x^{-p}}{x^{-p} + x^{-m} + x^{-n}} \quad \text{(Term 3)}

Step 4: Add the simplified terms Now, substitute the simplified terms back into the original expression: E=x−mx−m+x−n+x−p+x−nx−m+x−n+x−p+x−px−m+x−n+x−pE = \frac{x^{-m}}{x^{-m} + x^{-n} + x^{-p}} + \frac{x^{-n}}{x^{-m} + x^{-n} + x^{-p}} + \frac{x^{-p}}{x^{-m} + x^{-n} + x^{-p}} Since all three terms have the same denominator (x−m+x−n+x−p)(x^{-m} + x^{-n} + x^{-p}), we can add their numerators directly: E=x−m+x−n+x−px−m+x−n+x−pE = \frac{x^{-m} + x^{-n} + x^{-p}}{x^{-m} + x^{-n} + x^{-p}} Assuming x−m+x−n+x−p≠0x^{-m} + x^{-n} + x^{-p} \neq 0 (which is true if x>0x>0), the numerator and denominator are identical, so the expression simplifies to: E=1E = 1

The final answer is 1\boxed{\text{1}}.