Question

$\int 1^x.2^x.3^x.....n^x dx$

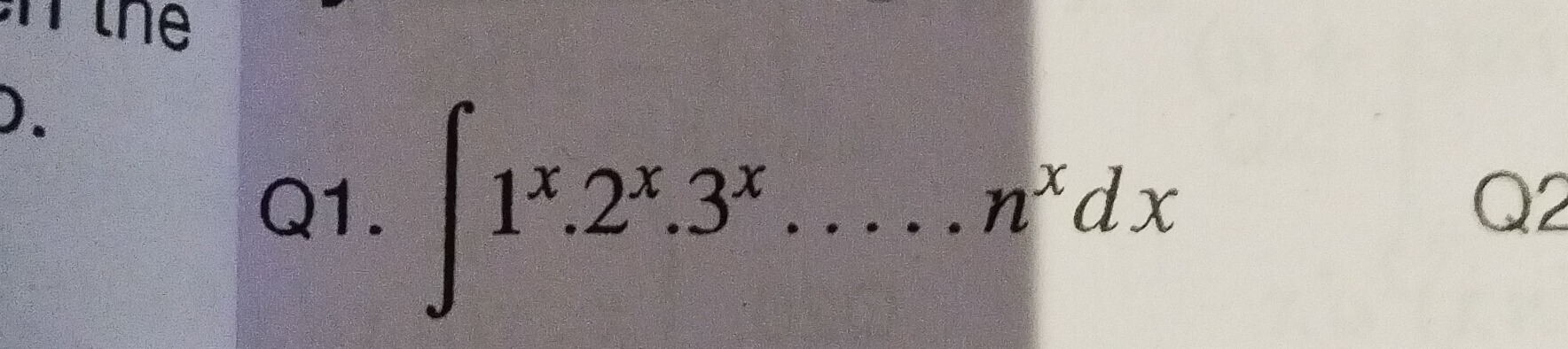
Answer 1

$\frac{(n!)^x}{\ln(n!)} + C$

Answer 2

The integrand $1^x.2^x.3^x.....n^x$ simplifies to $(1 \cdot 2 \cdot 3 \cdot \dots \cdot n)^x = (n!)^x$. The integral then becomes $\int (n!)^x dx$. This is a standard integral of the form $\int a^x dx$, where $a = n!$. Using the formula $\int a^x dx = \frac{a^x}{\ln a} + C$, we substitute $a = n!$ to get the result $\frac{(n!)^x}{\ln(n!)} + C$.