Question
Question: If p is a polynomial of 3 degree, $y^2 = p(x)$ and $Y = (tan^{-1}x)^2$, then which of the following ...
If p is a polynomial of 3 degree, y2=p(x) and Y=(tan−1x)2, then which of the following options is/are equal to
2dxd(y3dx2d2y)×((x2+1)2dx2d2Y+2x(1+x2)dxdY)?
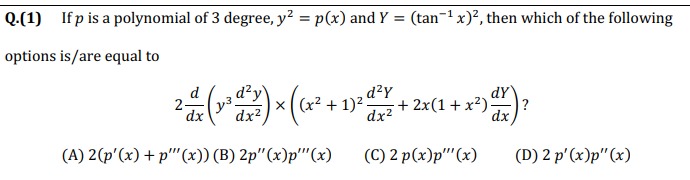
2(p′(x)+p′′′(x))
2p′′(x)p′′′(x)
2p(x)p′′′(x)
2p′(x)p′′(x)
2p(x)p′′′(x)
Solution
Let the given expression be E. We need to evaluate E=2dxd(y3dx2d2y)×((x2+1)2dx2d2Y+2x(1+x2)dxdY).
First, consider the term 2dxd(y3dx2d2y). We are given y2=p(x). Differentiating with respect to x: 2ydxdy=p′(x) Differentiating again with respect to x: 2ydx2d2y+2(dxdy)2=p′′(x) Differentiating a third time with respect to x: 2ydx3d3y+2dxdydx2d2y+4dxdydx2d2y=p′′′(x) 2ydx3d3y+6dxdydx2d2y=p′′′(x)
Now, evaluate dxd(y3dx2d2y): dxd(y3dx2d2y)=3y2dxdydx2d2y+y3dx3d3y So, 2dxd(y3dx2d2y)=2(3y2dxdydx2d2y+y3dx3d3y)=6y2dxdydx2d2y+2y3dx3d3y Factor out y2: 2dxd(y3dx2d2y)=y2(6dxdydx2d2y+2ydx3d3y) From the third derivative equation, 6dxdydx2d2y+2ydx3d3y=p′′′(x). Substituting this, we get: 2dxd(y3dx2d2y)=y2p′′′(x) Since y2=p(x), we have: 2dxd(y3dx2d2y)=p(x)p′′′(x).
Next, consider the term ((x2+1)2dx2d2Y+2x(1+x2)dxdY). We are given Y=(tan−1x)2. dxdY=dxd((tan−1x)2)=2(tan−1x)⋅1+x21=1+x22tan−1x. Let the second term be S=((x2+1)2dx2d2Y+2x(1+x2)dxdY). We can factor out (x2+1): S=(x2+1)[(x2+1)dx2d2Y+2xdxdY]. The expression in the square bracket is the derivative of the product (x2+1)dxdY: dxd((x2+1)dxdY)=(x2+1)dx2d2Y+2xdxdY. Let's evaluate (x2+1)dxdY: (x2+1)dxdY=(x2+1)(1+x22tan−1x)=2tan−1x. Now, differentiate this with respect to x: dxd((x2+1)dxdY)=dxd(2tan−1x)=1+x22. So, the expression in the square bracket is 1+x22. Substituting this back into S: S=(x2+1)[1+x22]=2.
Finally, the given expression E is the product of the two parts: E=(2dxd(y3dx2d2y))×((x2+1)2dx2d2Y+2x(1+x2)dxdY) E=(p(x)p′′′(x))×(2) E=2p(x)p′′′(x).
Comparing this with the given options: (A) 2(p′(x)+p′′′(x)) (B) 2p′′(x)p′′′(x) (C) 2p(x)p′′′(x) (D) 2p′(x)p′′(x)
The result matches option (C).
The final answer is 2p(x)p′′′(x).
The final answer is 2p(x)p′′′(x). The calculation for the first part 2dxd(y3dx2d2y) relies on the derivatives of y obtained from y2=p(x). The calculation for the second part ((x2+1)2dx2d2Y+2x(1+x2)dxdY) relies on the derivatives of Y=(tan−1x)2. The structure of the expression allows for simplification by recognizing it as (x2+1)×dxd((x2+1)dxdY).
