Question

Find the Integrals

(i) $\int \frac{\log x}{x^3}dx$ (ii)

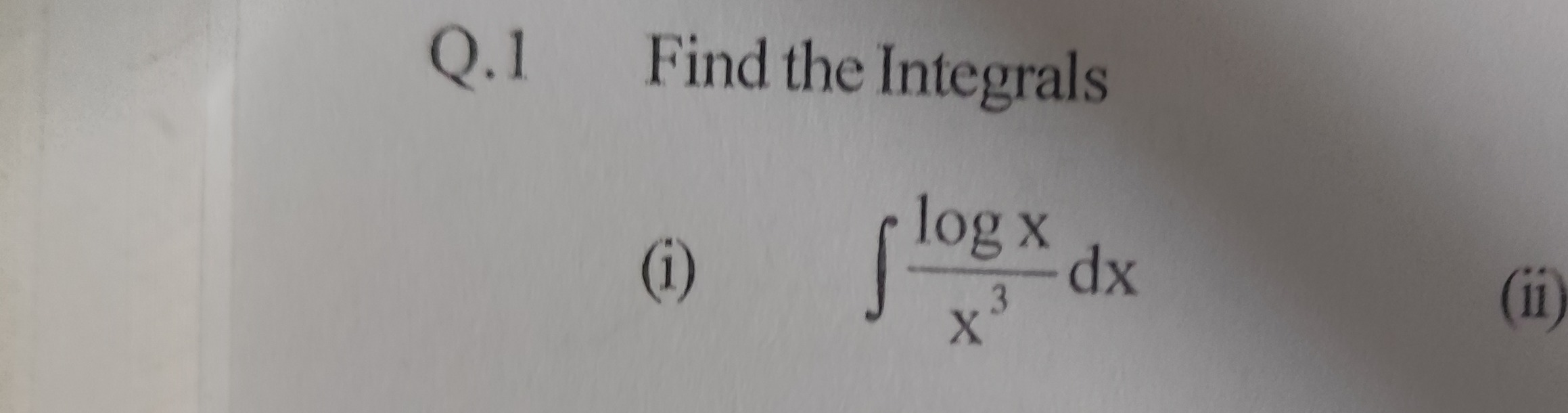
Answer 1

$\int \frac{\log x}{x^3} dx = -\frac{2\log x + 1}{4x^2} + C$

Answer 2

The integral can be solved using integration by parts formula: $\int u \, dv = uv - \int v \, du$.

Let $u = \log x$ and $dv = \frac{1}{x^3} dx = x^{-3} dx$.

Now, we find $du$ and $v$: $du = \frac{d}{dx}(\log x) dx = \frac{1}{x} dx$ $v = \int x^{-3} dx = \frac{x^{-3+1}}{-3+1} = \frac{x^{-2}}{-2} = -\frac{1}{2x^2}$

Substitute these into the integration by parts formula: $\int \frac{\log x}{x^3} dx = (\log x) \left(-\frac{1}{2x^2}\right) - \int \left(-\frac{1}{2x^2}\right) \left(\frac{1}{x}\right) dx$ $= -\frac{\log x}{2x^2} - \int \left(-\frac{1}{2x^3}\right) dx$ $= -\frac{\log x}{2x^2} + \frac{1}{2} \int x^{-3} dx$ Now, integrate $x^{-3}$: $\int x^{-3} dx = \frac{x^{-3+1}}{-3+1} = \frac{x^{-2}}{-2} = -\frac{1}{2x^2}$ Substitute this back into the expression: $= -\frac{\log x}{2x^2} + \frac{1}{2} \left(-\frac{1}{2x^2}\right) + C$ $= -\frac{\log x}{2x^2} - \frac{1}{4x^2} + C$ To combine the terms, find a common denominator: $= -\frac{2\log x}{4x^2} - \frac{1}{4x^2} + C$ $= -\frac{2\log x + 1}{4x^2} + C$