Question

Find relation between $x$, $y$ and $z$ if $x^2 + 9y^2 + 25z^2 = xyz\Bigl(\frac{15}{x} + \frac{5}{y} + \frac{3}{z}\Bigr)$

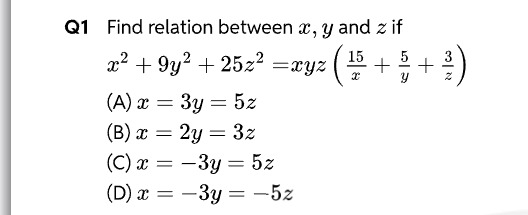
• A. $x = 3y = 5z$
• B. $x = 2y = 3z$
• C. $x = -3y = 5z$
• D. $x = -3y = -5z$

Answer 1

Answer: (A)

$x = 3y = 5z$

Answer 2

Step 1. Expand RHS:

$$xyz\Bigl(\frac{15}{x} + \frac{5}{y} + \frac{3}{z}\Bigr) =15\,yz + 5\,xz + 3\,xy.$$

Step 2. Bring all terms to one side:

$$x^2 - 5xz - 3xy + 9y^2 - 15yz + 25z^2 = 0.$$

Step 3. Test the option $x = 3y = 5z$.
Let $y = t$, then $x = 3t$, $z = \tfrac{3}{5}t$.

• LHS:

$$x^2 + 9y^2 + 25z^2 =9t^2 + 9t^2 + 25\Bigl(\tfrac{3}{5}t\Bigr)^2 =9t^2 + 9t^2 + 9t^2 = 27t^2.$$

• RHS:

$$xyz=3t \cdot t \cdot \tfrac{3}{5}t = \frac{9}{5}t^3, \quad \frac{15}{x} + \frac{5}{y} + \frac{3}{z} =\frac{15}{3t} + \frac{5}{t} + \frac{3}{\tfrac{3}{5}t} =5/t + 5/t + 5/t = 15/t.$$ $$\text{RHS} = \frac{9}{5}t^3 \times \frac{15}{t} = 27t^2.$$

Since LHS = RHS, the relation holds only for $x=3y=5z$.