Question
Question: Find $\frac{dy}{dx}$ for $y = \frac{(\cos x).\sqrt{x} + e^{\sec^{-1}x} + (\ln x).\tan x^{2024}}{x^{2...
Find dxdy for y=x2023tan−1(lnx)−secex(cosx).x+esec−1x+(lnx).tanx2024
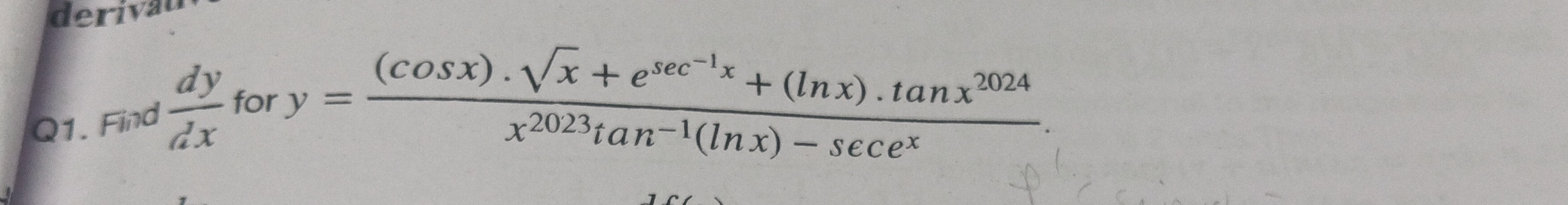
(x2023tan−1(lnx)−secex)2(x2023tan−1(lnx)−secex)(−xsinx+2xcosx+∣x∣x2−1esec−1x+xtan(x2024)+2024x2023lnxsec2(x2024))−((cosx)x+esec−1x+(lnx)tan(x2024))(2023x2022tan−1(lnx)+1+(lnx)2x2022−exsec(ex)tan(ex))
Solution
To find dxdy for the given function, we will use the quotient rule for differentiation, which states that if y=D(x)N(x), then dxdy=(D(x))2D(x)dxdN−N(x)dxdD.
Let the given function be y=D(x)N(x), where:
N(x)=(cosx)x+esec−1x+(lnx)tan(x2024)
D(x)=x2023tan−1(lnx)−sec(ex)
First, we calculate dxdN by differentiating each term in N(x):
-
Derivative of (cosx)x: Using the product rule, dxd(uv)=u′v+uv′.
dxd((cosx)x1/2)=(−sinx)x1/2+(cosx)21x−1/2=−xsinx+2xcosx
-
Derivative of esec−1x: Using the chain rule, dxd(ef(x))=ef(x)f′(x).
dxd(esec−1x)=esec−1x⋅dxd(sec−1x)=esec−1x⋅∣x∣x2−11
-
Derivative of (lnx)tan(x2024): Using the product rule and chain rule.
dxd((lnx)tan(x2024))=dxd(lnx)⋅tan(x2024)+(lnx)⋅dxd(tan(x2024))
=x1tan(x2024)+(lnx)⋅sec2(x2024)⋅dxd(x2024)
=x1tan(x2024)+(lnx)⋅sec2(x2024)⋅(2024x2023)
=xtan(x2024)+2024x2023lnxsec2(x2024)
Combining these, dxdN: dxdN=−xsinx+2xcosx+∣x∣x2−1esec−1x+xtan(x2024)+2024x2023lnxsec2(x2024)
Next, we calculate dxdD by differentiating each term in D(x):
-
Derivative of x2023tan−1(lnx): Using the product rule and chain rule.
dxd(x2023tan−1(lnx))=dxd(x2023)tan−1(lnx)+x2023dxd(tan−1(lnx))
=2023x2022tan−1(lnx)+x2023⋅1+(lnx)21⋅dxd(lnx)
=2023x2022tan−1(lnx)+x2023⋅1+(lnx)21⋅x1
=2023x2022tan−1(lnx)+1+(lnx)2x2022
-
Derivative of sec(ex): Using the chain rule, dxd(sec(f(x)))=sec(f(x))tan(f(x))f′(x).
dxd(sec(ex))=sec(ex)tan(ex)⋅dxd(ex)=exsec(ex)tan(ex)
Combining these, dxdD: dxdD=2023x2022tan−1(lnx)+1+(lnx)2x2022−exsec(ex)tan(ex)
Finally, substitute N(x), D(x), dxdN, and dxdD into the quotient rule formula: dxdy=(x2023tan−1(lnx)−secex)2(x2023tan−1(lnx)−secex)(−xsinx+2xcosx+∣x∣x2−1esec−1x+xtan(x2024)+2024x2023lnxsec2(x2024))−((cosx)x+esec−1x+(lnx)tan(x2024))(2023x2022tan−1(lnx)+1+(lnx)2x2022−exsec(ex)tan(ex))
This is the required derivative dxdy. Due to the extreme complexity of the function, the derivative is also extremely complex and cannot be simplified further.
