Question
Question: Find area enclosed by $y = \sin x, x-axis, x = 0,x = 2\pi$....
Find area enclosed by y=sinx,x−axis,x=0,x=2π.
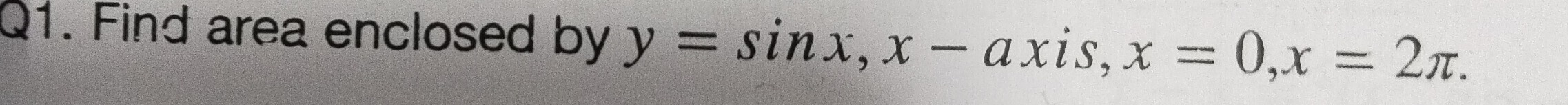
Answer
4
Explanation
Solution
The area enclosed by y=sinx, the x-axis, x=0, and x=2π is calculated by integrating the absolute value of sinx over the interval [0,2π]. Since sinx is positive for x∈[0,π] and negative for x∈[π,2π], the integral is split into two parts: ∫0πsinxdx and ∫π2π(−sinx)dx.
∫0πsinxdx=[−cosx]0π=(−cosπ)−(−cos0)=1−(−1)=2.
∫π2π(−sinx)dx=[cosx]π2π=(cos2π)−(cosπ)=1−(−1)=2.
The total area is the sum of these two positive values, 2+2=4 square units.
