Question

f and g be two positive real valued functions defined on [-1,1] such that $f(-x) = \frac{1}{f(x)}$ and g is an even function with $\int_{-1}^{1} g(x)dx = 1$ then $I = \int_{-1}^{1} f(x)g(x)dx$ satisfies

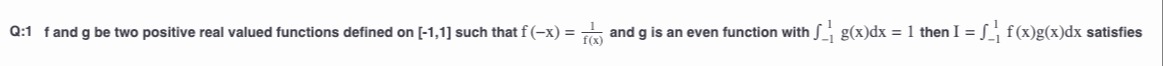
• A. I < 2
• B. I > 2
• C. I = 1
• D. I ≥ 1

Answer 1

Answer: (D)

I ≥ 1

Answer 2

We are given that:

• $f(-x)=\frac{1}{f(x)}$ for all $x \in [-1,1]$ and $f(x)>0$,
• $g$ is even, i.e., $g(-x) = g(x)$,
• $\displaystyle \int_{-1}^{1} g(x) \, dx = 1$.

Let

$$I = \int_{-1}^{1} f(x)g(x) \, dx.$$

Substitute $x \to -x$:

$$I = \int_{-1}^{1} f(-x)g(-x) \, dx = \int_{-1}^{1} \frac{1}{f(x)}g(x) \, dx.$$

Thus, we have

$$I = \int_{-1}^{1} \frac{1}{f(x)}g(x) \, dx.$$

Adding the two expressions:

$$2I = \int_{-1}^{1} \left(f(x) + \frac{1}{f(x)}\right)g(x) \, dx.$$

Since $f(x)>0$,

$$f(x) + \frac{1}{f(x)} \geq 2 \quad \text{(AM-GM inequality)},$$

with equality if and only if $f(x)=1$.

Therefore,

$$2I \geq \int_{-1}^{1} 2\,g(x)\,dx = 2\int_{-1}^{1} g(x)\,dx = 2,$$

which gives:

$$I \geq 1.$$