Question
Question: $\begin{matrix} \log_3 512 & \log_2 3 & \log_8 3\\ \log_4 3 & \log_3 4 & \log_3 4\\ \log_3 8 & \log...
log3512log43log38log23log34log49log83log34 is equal to
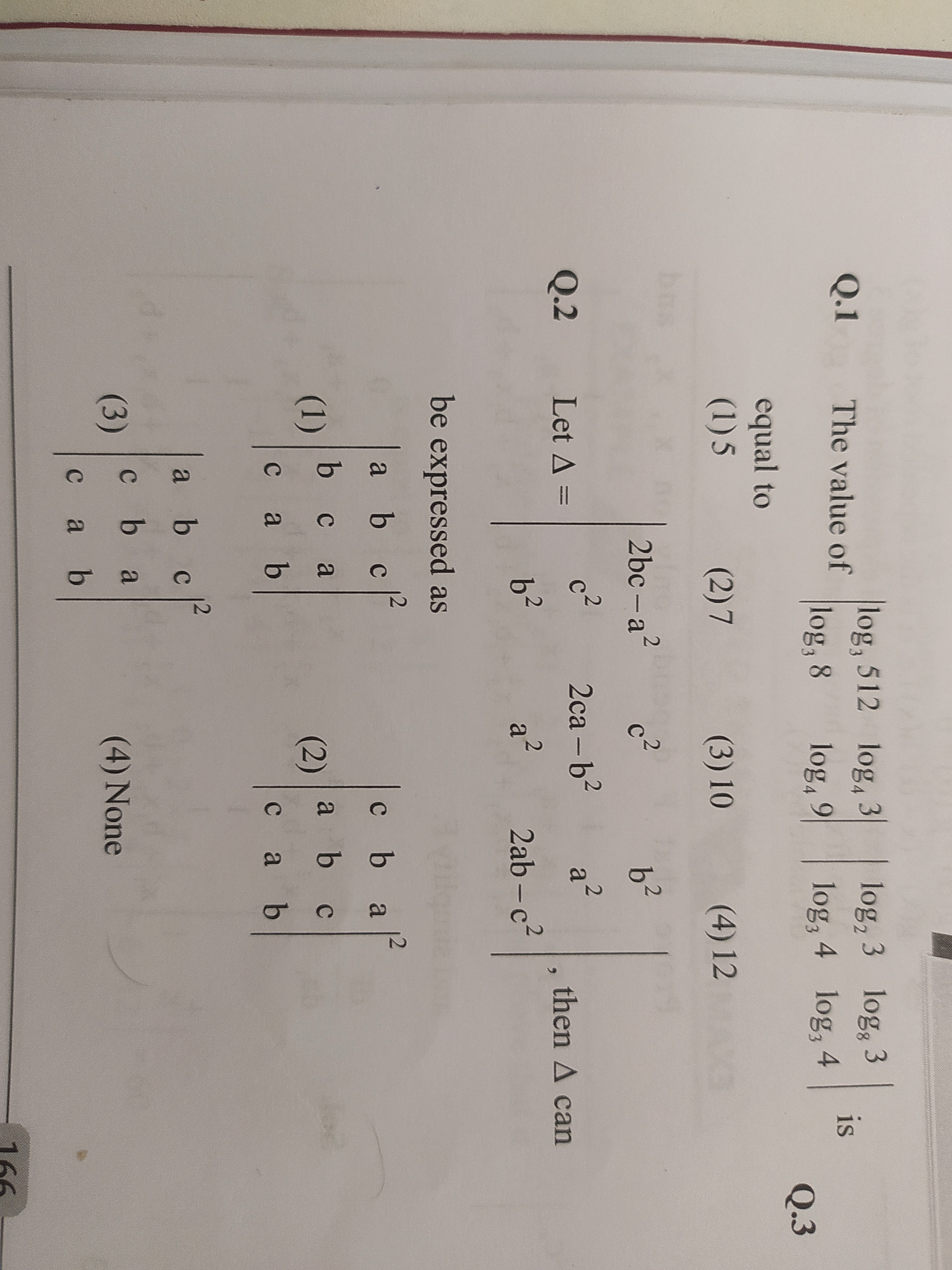
5
7
10
12
There appears to be an error in the question statement or the provided options, as the determinant does not simplify to a constant integer value based on standard calculations. Without clarification or correction of the question, it is not possible to definitively choose one of the integer options.
Solution
The determinant is given by
Δ=log3512log43log38log23log34log49log83log34log364
Using logarithm properties logban=nlogba, logbma=m1logba, and logba=logab1, we can rewrite the entries.
Let x=log32. Then log23=log321=x1.
The entries become:
log3512=log329=9log32=9x
log23=1/x
log83=log233=31log23=3x1
log43=log223=21log23=2x1
log34=log322=2log32=2x
log38=log323=3log32=3x
log49=log2232=22log23=log23=1/x
log364=log326=6log32=6x
The determinant is:
Δ=9x1/(2x)3x1/x2x1/x1/(3x)2x6x
Expanding the determinant:
Δ=9x[(2x)(6x)−(2x)(1/x)]−1/x[(1/(2x))(6x)−(2x)(3x)]+1/(3x)[(1/(2x))(1/x)−(2x)(3x)]
Δ=9x[12x2−2]−1/x[3−6x2]+1/(3x)[1/(2x2)−6x2]
Δ=(108x3−18x)−(3/x−6x)+(1/(6x3)−2x)
Δ=108x3−18x−3/x+6x+1/(6x3)−2x
Δ=108x3−14x−3/x+1/(6x3)
Where x=log32. This expression is generally not an integer and depends on the value of x. Given that the options are integers, there is likely an error in the question statement or the provided options, as the determinant does not simplify to a constant integer value based on standard calculations. Without clarification or correction of the question, it is not possible to definitively choose one of the integer options.
