Question
Question: $\begin{array}{l}\log_{3} 512\\\log_{3} 8\end{array}$ $\begin{array}{l}\log_{2} 3\\\log_{4} 3\end{ar...
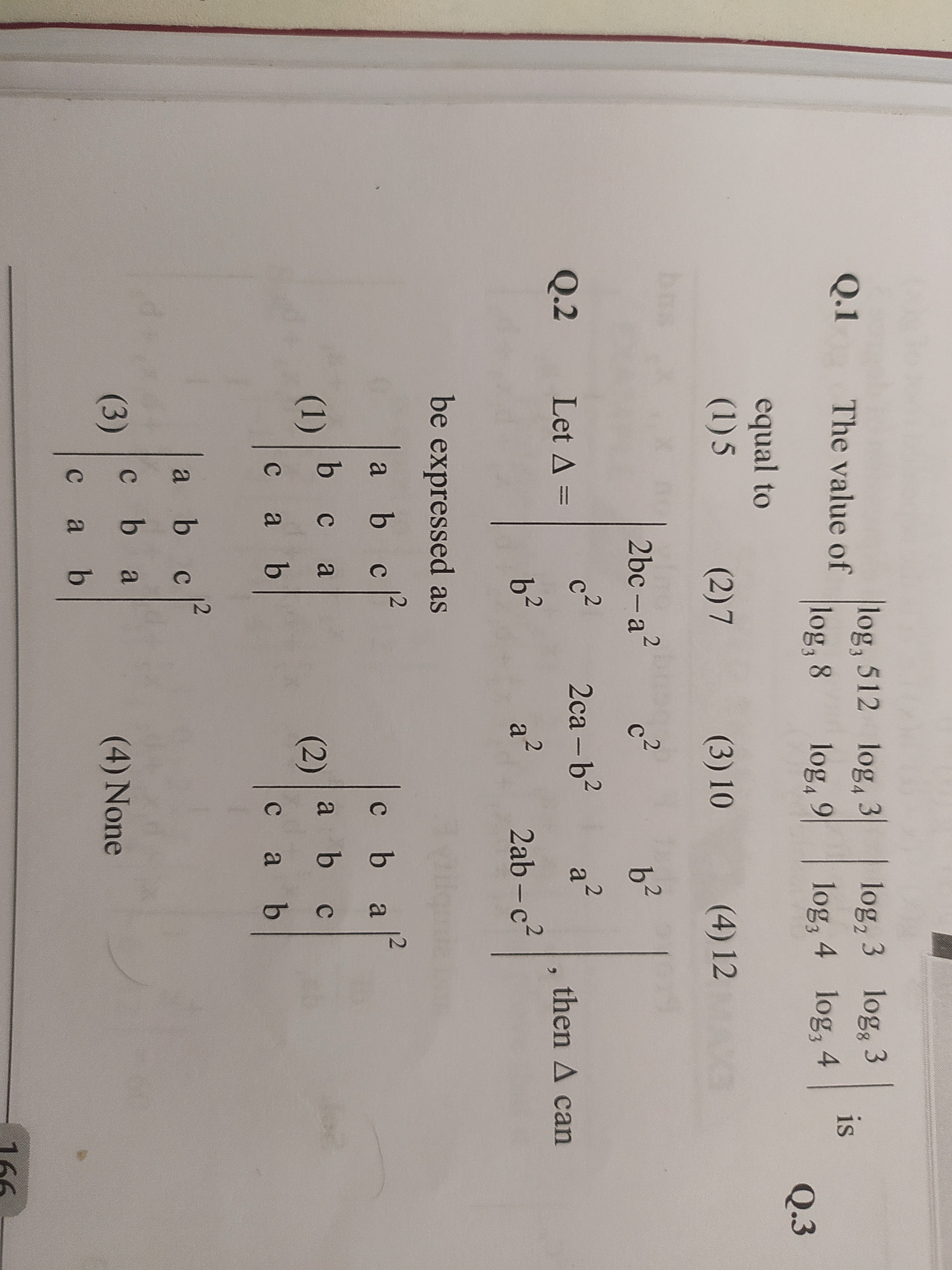
log3512log38 log23log43 log83log34 is log35log49 equal to
A
5
B
7
C
10
D
12
Answer
10
Explanation
Solution
The question is interpreted as the product of two determinants. The first determinant is log3512log38log43log49. Evaluating the terms using logarithm properties: log3512=9log32, log43=21log23, log38=3log32, log49=log23. The determinant is (9log32)(log23)−(21log23)(3log32)=9−23=215.
The second determinant is log23log34log83log34. Evaluating the terms: log23, log83=31log23, log34=2log32. The determinant is (log23)(2log32)−(31log23)(2log32)=2−32=34.
The product is 215×34=10.
