Question
Question: A finite conducting wire XY carries a current $I$. The magnetic field $d\overrightarrow{B}$ due to i...
A finite conducting wire XY carries a current I. The magnetic field dB due to infinitesimal element dl of the conducting wire at a point P as shown in figure is:
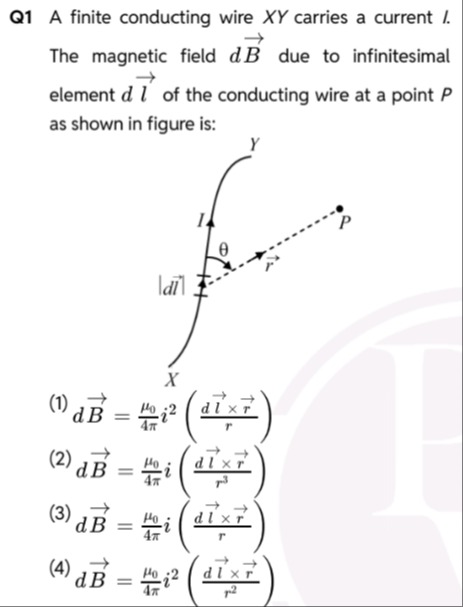
dB=4πμ0i2(rdl×r)
dB=4πμ0i(r3dl×r)
dB=4πμ0i(rdl×r)
dB=4πμ0i2(r2dl×r)
(2)
Solution
The magnetic field dB produced by an infinitesimal current element Idl at a point P located at a position vector r relative to the element is given by the Biot-Savart Law: dB=4πμ0r3Idl×r where μ0 is the permeability of free space, I is the current, dl is the vector representing the infinitesimal length of the wire element, r is the position vector from the wire element to the point P, and r=∣r∣ is the distance from the element to the point.
In the given question, the current is denoted by I in the text, but by i in the options. Assuming i in the options represents the current I, the Biot-Savart Law becomes: dB=4πμ0r3idl×r
Comparing this formula with the given options: (1) dB=4πμ0i2(rdl×r): Incorrect. The current dependence is i2 instead of i, and the denominator is r instead of r3. (2) dB=4πμ0i(r3dl×r): Correct. This matches the Biot-Savart Law. (3) dB=4πμ0i(rdl×r): Incorrect. The denominator is r instead of r3. (4) dB=4πμ0i2(r2dl×r): Incorrect. The current dependence is i2 instead of i, and the denominator is r2 instead of r3.
Therefore, option (2) is the correct expression for the magnetic field dB.
