Question
Question: Q. $v = 2sin(t)\hat{i} + 2cos(t)\hat{j}$ find i) $accl^n$ at $t = \frac{\pi}{6}$ sec. ii) $\overrig...
Q. v=2sin(t)i^+2cos(t)j^ find i) accln at t=6π sec.
ii) S at 6π sec sec.
if Particle started at t=0sec.
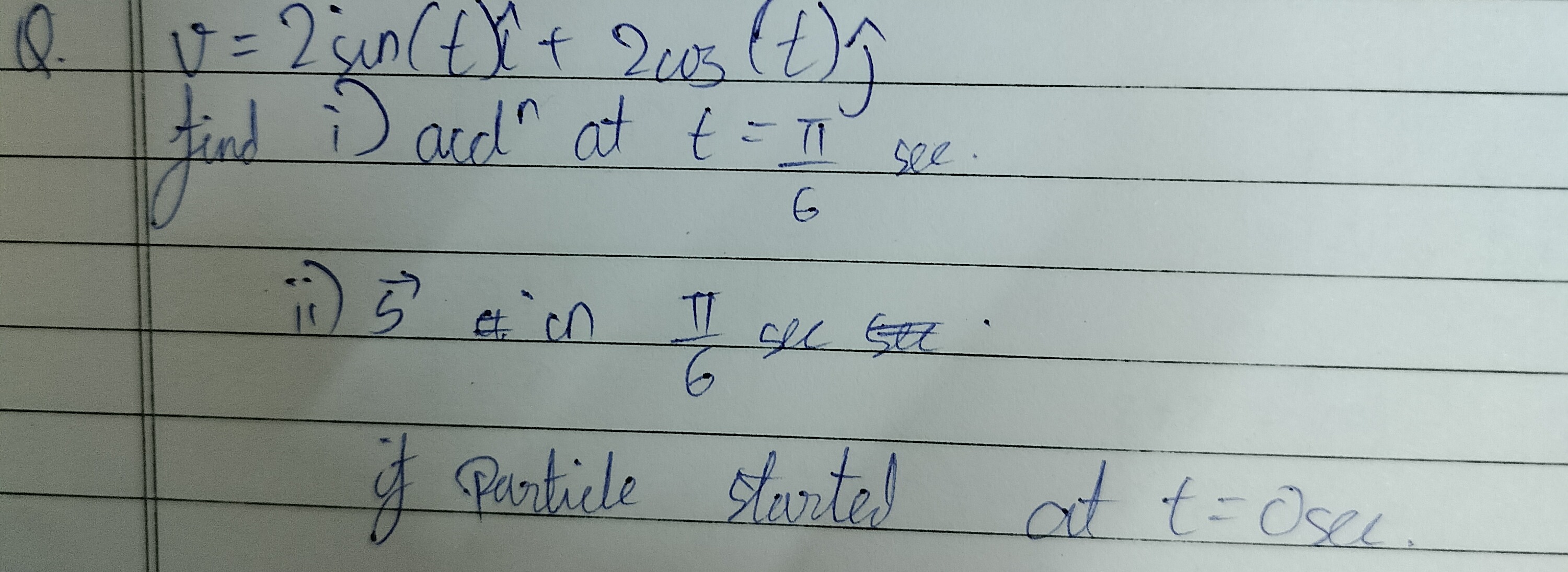
i) 3i^−j^ ii) (2−3)i^+j^
Solution
i) Acceleration is the time derivative of velocity. Differentiate the given velocity vector v(t) with respect to t to get a(t). Substitute t=6π into a(t) and evaluate the trigonometric functions cos(6π) and sin(6π) to find the acceleration vector at that time.
ii) Displacement is the change in position. The displacement vector from time t1 to t2 is the definite integral of the velocity vector from t1 to t2. Here, t1=0 and t2=6π. Integrate the given velocity vector v(t) with respect to t from 0 to 6π. Evaluate the definite integral by substituting the limits and subtracting the value at the lower limit from the value at the upper limit. This gives the displacement vector at t=6π sec relative to the position at t=0 sec.
