Question

The solution of $\frac{dy}{dx} = \frac{e^x(\sin^2x + \sin2x)}{y(2\log y + 1)}$ is

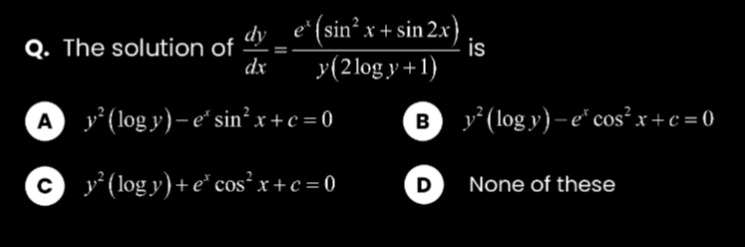
• A. $y^2(\log y) - e^x\sin^2x + c = 0$
• B. $y^2(\log y) - e^x\cos^2x + c = 0$
• C. $y^2(\log y) + e^x\cos^2x + c = 0$
• D. None of these

Answer 1

Answer: (A)

A

Answer 2

The given differential equation is: $\frac{dy}{dx} = \frac{e^x(\sin^2x + \sin2x)}{y(2\log y + 1)}$

This is a separable differential equation. We can rearrange the terms to separate variables $x$ and $y$: $y(2\log y + 1) dy = e^x(\sin^2x + \sin2x) dx$

Now, integrate both sides: $\int y(2\log y + 1) dy = \int e^x(\sin^2x + \sin2x) dx$

Let's evaluate the Left Hand Side (LHS) integral: $\text{LHS} = \int (2y\log y + y) dy$ We can split this into two integrals: $\int 2y\log y dy + \int y dy$.

For the integral $\int 2y\log y dy$, we use integration by parts, $\int u dv = uv - \int v du$. Let $u = \log y$ and $dv = 2y dy$. Then $du = \frac{1}{y} dy$ and $v = y^2$. So, $\int 2y\log y dy = (\log y)(y^2) - \int y^2 \left(\frac{1}{y}\right) dy$ $= y^2 \log y - \int y dy$ $= y^2 \log y - \frac{y^2}{2}$

Now, substitute this back into the LHS integral: $\text{LHS} = \left(y^2 \log y - \frac{y^2}{2}\right) + \frac{y^2}{2} + C_1$ $\text{LHS} = y^2 \log y + C_1$

Next, let's evaluate the Right Hand Side (RHS) integral: $\text{RHS} = \int e^x(\sin^2x + \sin2x) dx$ We know that $\sin2x = 2\sin x \cos x$. So the integral becomes: $\text{RHS} = \int e^x(\sin^2x + 2\sin x \cos x) dx$ This integral is of the form $\int e^x(f(x) + f'(x)) dx$, which evaluates to $e^x f(x) + C$. Here, let $f(x) = \sin^2x$. Then, $f'(x) = \frac{d}{dx}(\sin^2x) = 2\sin x \cdot \cos x = \sin2x$. Thus, the integral fits the form. $\text{RHS} = e^x \sin^2x + C_2$

Equating the LHS and RHS results: $y^2 \log y + C_1 = e^x \sin^2x + C_2$ Rearranging the terms and combining the constants into a single constant $C = C_2 - C_1$: $y^2 \log y - e^x \sin^2x + C = 0$

Comparing this result with the given options, the derived solution matches option A.