Solveeit Logo
Login

Question

Question: Shown are the initial voltages on each capacitor. Find out the final charges if A is joined to F, B ...

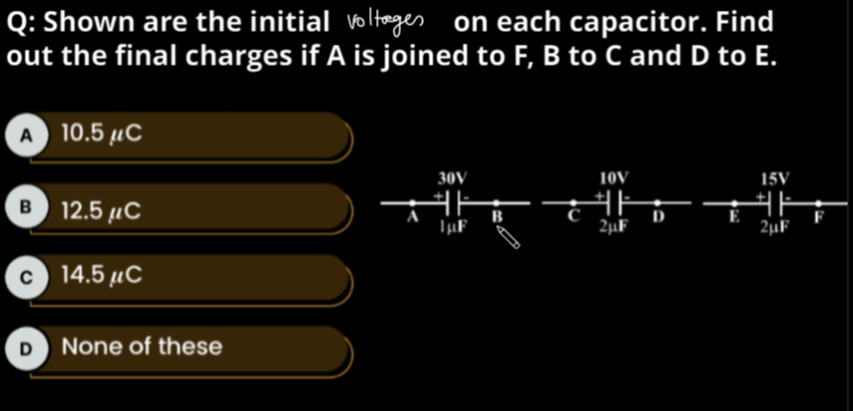
Shown are the initial voltages on each capacitor. Find out the final charges if A is joined to F, B to C and D to E.

A

10.5 μC\mu C

B

12.5 μC\mu C

C

14.5 μC\mu C

D

None of these

Answer

12.5 μC\mu C

Explanation

Solution

The initial charges on the capacitor plates are:

Q1A=+C1V1=+1μF×30V=+30μCQ_{1A} = +C_1 V_1 = +1 \mu F \times 30 V = +30 \mu C

Q1B=−C1V1=−1μF×30V=−30μCQ_{1B} = -C_1 V_1 = -1 \mu F \times 30 V = -30 \mu C

Q2C=+C2V2=+2μF×10V=+20μCQ_{2C} = +C_2 V_2 = +2 \mu F \times 10 V = +20 \mu C

Q2D=−C2V2=−2μF×10V=−20μCQ_{2D} = -C_2 V_2 = -2 \mu F \times 10 V = -20 \mu C

Q3E=+C3V3=+2μF×15V=+30μCQ_{3E} = +C_3 V_3 = +2 \mu F \times 15 V = +30 \mu C

Q3F=−C3V3=−2μF×15V=−30μCQ_{3F} = -C_3 V_3 = -2 \mu F \times 15 V = -30 \mu C

When A is joined to F, B to C, and D to E, we form three connected nodes: (A, F), (B, C), and (D, E). Let their final potentials be VAFV_{AF}, VBCV_{BC}, and VDEV_{DE}. The final voltages across the capacitors are:

V1f=VA−VB=VAF−VBCV_{1f} = V_A - V_B = V_{AF} - V_{BC}

V2f=VC−VD=VBC−VDEV_{2f} = V_C - V_D = V_{BC} - V_{DE}

V3f=VE−VF=VDE−VAFV_{3f} = V_E - V_F = V_{DE} - V_{AF}

The final charges on the plates are:

Q1f=C1V1f=C1(VAF−VBC)Q_{1f} = C_1 V_{1f} = C_1 (V_{AF} - V_{BC}) (charge on plate A)

−Q1f=−C1V1f=−C1(VAF−VBC)-Q_{1f} = -C_1 V_{1f} = -C_1 (V_{AF} - V_{BC}) (charge on plate B)

Q2f=C2V2f=C2(VBC−VDE)Q_{2f} = C_2 V_{2f} = C_2 (V_{BC} - V_{DE}) (charge on plate C)

−Q2f=−C2V2f=−C2(VBC−VDE)-Q_{2f} = -C_2 V_{2f} = -C_2 (V_{BC} - V_{DE}) (charge on plate D)

Q3f=C3V3f=C3(VDE−VAF)Q_{3f} = C_3 V_{3f} = C_3 (V_{DE} - V_{AF}) (charge on plate E)

−Q3f=−C3V3f=−C3(VDE−VAF)-Q_{3f} = -C_3 V_{3f} = -C_3 (V_{DE} - V_{AF}) (charge on plate F)

By conservation of charge on each connected node:

Node (B, C): Initial charge Q1B+Q2C=−30+20=−10μCQ_{1B} + Q_{2C} = -30 + 20 = -10 \mu C. Final charge −Q1f+Q2f=−C1(VAF−VBC)+C2(VBC−VDE)-Q_{1f} + Q_{2f} = -C_1(V_{AF} - V_{BC}) + C_2(V_{BC} - V_{DE}).

−1(VAF−VBC)+2(VBC−VDE)=−10-1(V_{AF} - V_{BC}) + 2(V_{BC} - V_{DE}) = -10

−VAF+VBC+2VBC−2VDE=−10  ⟹  −VAF+3VBC−2VDE=−10-V_{AF} + V_{BC} + 2V_{BC} - 2V_{DE} = -10 \implies -V_{AF} + 3V_{BC} - 2V_{DE} = -10 (1)

Node (D, E): Initial charge Q2D+Q3E=−20+30=10μCQ_{2D} + Q_{3E} = -20 + 30 = 10 \mu C. Final charge −Q2f+Q3f=−C2(VBC−VDE)+C3(VDE−VAF)-Q_{2f} + Q_{3f} = -C_2(V_{BC} - V_{DE}) + C_3(V_{DE} - V_{AF}).

−2(VBC−VDE)+2(VDE−VAF)=10-2(V_{BC} - V_{DE}) + 2(V_{DE} - V_{AF}) = 10

−2VBC+2VDE+2VDE−2VAF=10  ⟹  −2VAF−2VBC+4VDE=10  ⟹  −VAF−VBC+2VDE=5-2V_{BC} + 2V_{DE} + 2V_{DE} - 2V_{AF} = 10 \implies -2V_{AF} - 2V_{BC} + 4V_{DE} = 10 \implies -V_{AF} - V_{BC} + 2V_{DE} = 5 (2)

Node (A, F): Initial charge Q1A+Q3F=30+(−30)=0μCQ_{1A} + Q_{3F} = 30 + (-30) = 0 \mu C. Final charge Q1f−Q3f=C1(VAF−VBC)−C3(VDE−VAF)Q_{1f} - Q_{3f} = C_1(V_{AF} - V_{BC}) - C_3(V_{DE} - V_{AF}).

1(VAF−VBC)−2(VDE−VAF)=01(V_{AF} - V_{BC}) - 2(V_{DE} - V_{AF}) = 0

VAF−VBC−2VDE+2VAF=0  ⟹  3VAF−VBC−2VDE=0V_{AF} - V_{BC} - 2V_{DE} + 2V_{AF} = 0 \implies 3V_{AF} - V_{BC} - 2V_{DE} = 0 (3)

We have the system of equations:

(1) −VAF+3VBC−2VDE=−10-V_{AF} + 3V_{BC} - 2V_{DE} = -10

(2) −VAF−VBC+2VDE=5-V_{AF} - V_{BC} + 2V_{DE} = 5

(3) 3VAF−VBC−2VDE=03V_{AF} - V_{BC} - 2V_{DE} = 0

Adding (1) and (2): (−VAF+3VBC−2VDE)+(−VAF−VBC+2VDE)=−10+5  ⟹  −2VAF+2VBC=−5  ⟹  2VAF−2VBC=5(-V_{AF} + 3V_{BC} - 2V_{DE}) + (-V_{AF} - V_{BC} + 2V_{DE}) = -10 + 5 \implies -2V_{AF} + 2V_{BC} = -5 \implies 2V_{AF} - 2V_{BC} = 5 (4) Adding (2) and (3): (−VAF−VBC+2VDE)+(3VAF−VBC−2VDE)=5+0  ⟹  2VAF−2VBC=5(-V_{AF} - V_{BC} + 2V_{DE}) + (3V_{AF} - V_{BC} - 2V_{DE}) = 5 + 0 \implies 2V_{AF} - 2V_{BC} = 5 (5) Equations (4) and (5) are identical, indicating linear dependence. This is expected because the sum of initial charges on all plates is 30−30+20−20+30−30=030-30+20-20+30-30 = 0, and the sum of final charges is Q1f−Q1f+Q2f−Q2f+Q3f−Q3f=0Q_{1f} - Q_{1f} + Q_{2f} - Q_{2f} + Q_{3f} - Q_{3f} = 0. Also, V1f+V2f+V3f=0V_{1f} + V_{2f} + V_{3f} = 0.

We can use the potential of one node as a reference, say VDE=0V_{DE} = 0. Then the equations become:

(1) −VAF+3VBC=−10-V_{AF} + 3V_{BC} = -10

(2) −VAF−VBC=5-V_{AF} - V_{BC} = 5

(3) 3VAF−VBC=03V_{AF} - V_{BC} = 0

From (3), VBC=3VAFV_{BC} = 3V_{AF}. Substitute into (2): −VAF−3VAF=5  ⟹  −4VAF=5  ⟹  VAF=−5/4=−1.25V-V_{AF} - 3V_{AF} = 5 \implies -4V_{AF} = 5 \implies V_{AF} = -5/4 = -1.25 V. Then VBC=3×(−1.25)=−3.75VV_{BC} = 3 \times (-1.25) = -3.75 V. Check with (1): −(−1.25)+3(−3.75)=1.25−11.25=−10-(-1.25) + 3(-3.75) = 1.25 - 11.25 = -10. This is consistent. So, VAF=−1.25VV_{AF} = -1.25 V, VBC=−3.75VV_{BC} = -3.75 V, VDE=0VV_{DE} = 0 V.

The final voltages across the capacitors are:

V1f=VAF−VBC=−1.25−(−3.75)=−1.25+3.75=2.5VV_{1f} = V_{AF} - V_{BC} = -1.25 - (-3.75) = -1.25 + 3.75 = 2.5 V.

V2f=VBC−VDE=−3.75−0=−3.75VV_{2f} = V_{BC} - V_{DE} = -3.75 - 0 = -3.75 V.

V3f=VDE−VAF=0−(−1.25)=1.25VV_{3f} = V_{DE} - V_{AF} = 0 - (-1.25) = 1.25 V.

The final charges on the positive plates are:

Q1f=C1V1f=1μF×2.5V=2.5μCQ_{1f} = C_1 V_{1f} = 1 \mu F \times 2.5 V = 2.5 \mu C.

Q2f=C2V2f=2μF×(−3.75V)=−7.5μCQ_{2f} = C_2 V_{2f} = 2 \mu F \times (-3.75 V) = -7.5 \mu C.

Q3f=C3V3f=2μF×1.25V=2.5μCQ_{3f} = C_3 V_{3f} = 2 \mu F \times 1.25 V = 2.5 \mu C.

The magnitudes of the final charges are ∣Q1f∣=2.5μC|Q_{1f}| = 2.5 \mu C, ∣Q2f∣=7.5μC|Q_{2f}| = 7.5 \mu C, ∣Q3f∣=2.5μC|Q_{3f}| = 2.5 \mu C. The sum of the magnitudes is 2.5+7.5+2.5=12.5μC2.5 + 7.5 + 2.5 = 12.5 \mu C. Therefore, the final answer is the sum of magnitudes of final charges.