Question

$\left(\frac{1}{y}\sin\frac{x}{y}-\frac{y}{x^2}\cos\frac{y}{x}+1\right)dx+\left(\frac{1}{x}\cos\frac{y}{x}-\frac{x}{y^2}\sin\frac{x}{y}+\frac{1}{y^2}\right)dy=0$

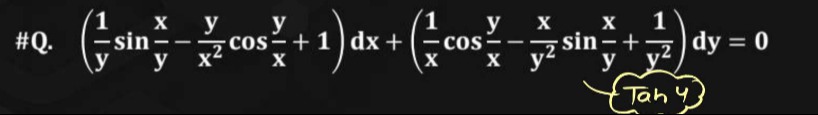
Answer 1

$x + \sin\frac{y}{x} - \cos\frac{x}{y} - \frac{1}{y} = C$

Answer 2

The given differential equation is exact because $\frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}$. The general solution is found by integrating $M$ with respect to $x$ and $N$ with respect to $y$, and combining the results. The integrated form is $F(x, y) = \int M dx + \int N_{rem} dy = C$, where $N_{rem}$ are the terms in $N$ not present in $\frac{\partial}{\partial y} \int M dx$. In this case, $F(x, y) = -\cos\frac{x}{y} + \sin\frac{y}{x} + x - \frac{1}{y} = C$.