Question
Question: L $\lim_{n \to \infty} \frac{1}{\sqrt{n^2-1}} + \frac{1}{\sqrt{n^2-4}} + \frac{1}{\sqrt{n^2-9}} + \d...
L limn→∞n2−11+n2−41+n2−91+⋯+2n−11
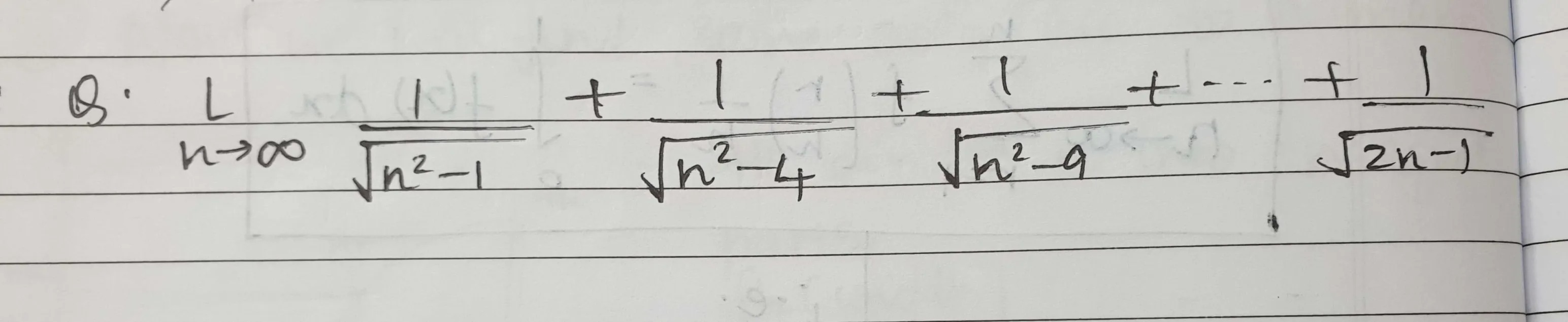
Answer
2π
Explanation
Solution
The given sum can be written as Sn=∑k=1n−1n2−k21. We can rewrite the general term by factoring out n2 from the square root: n2−k21=n2(1−n2k2)1=n1−(nk)21 So, the sum becomes: Sn=∑k=1n−1n1⋅1−(nk)21 This is a Riemann sum for the function f(x)=1−x21 over the interval [0,1]. As n→∞, the limit of this sum is the definite integral: L=limn→∞Sn=∫011−x21dx The integral of 1−x21 is arcsin(x). Evaluating the definite integral: ∫011−x21dx=[arcsin(x)]01=arcsin(1)−arcsin(0)=2π−0=2π Therefore, the limit is 2π.
