Question

In the given diagram, what does the shaded area represent?

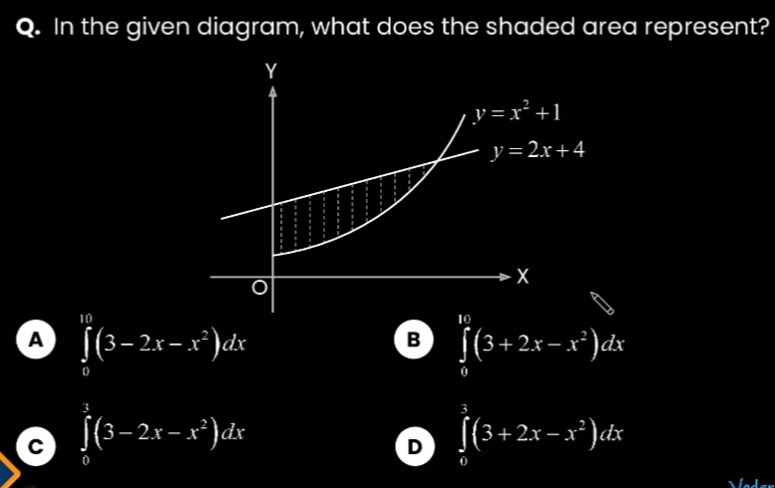
• A. $\int_{0}^{10}(3-2x-x^2)dx$
• B. $\int_{0}^{10}(3+2x-x^2)dx$
• C. $\int_{0}^{3}(3-2x-x^2)dx$
• D. $\int_{0}^{3}(3+2x-x^2)dx$

Answer 1

Answer: (D)

$\int_{0}^{3}(3+2x-x^2)dx$

Answer 2

The shaded area is the region between the curves $y = 2x + 4$ and $y = x^2 + 1$.

1. Find intersection points: $x^2 + 1 = 2x + 4 \implies x^2 - 2x - 3 = 0 \implies (x-3)(x+1)=0$. Intersection points are $x=3$ and $x=-1$.
2. From the diagram, the shaded region extends from $x=0$ to $x=3$. So, the limits of integration are $0$ to $3$.
3. In the interval $[0, 3]$, test a point (e.g., $x=1$): $y_{line}(1) = 2(1)+4=6$, $y_{parabola}(1) = 1^2+1=2$. Since $6 > 2$, the line $y = 2x+4$ is above the parabola $y = x^2+1$.
4. The area is given by $\int_{a}^{b} (y_{upper} - y_{lower}) dx$. Area $= \int_{0}^{3} ((2x + 4) - (x^2 + 1)) dx$ Area $= \int_{0}^{3} (2x + 4 - x^2 - 1) dx$ Area $= \int_{0}^{3} (3 + 2x - x^2) dx$