Question
Question: In the given circuit diagram, a wire is joining points B and D. The current in this wire is:...
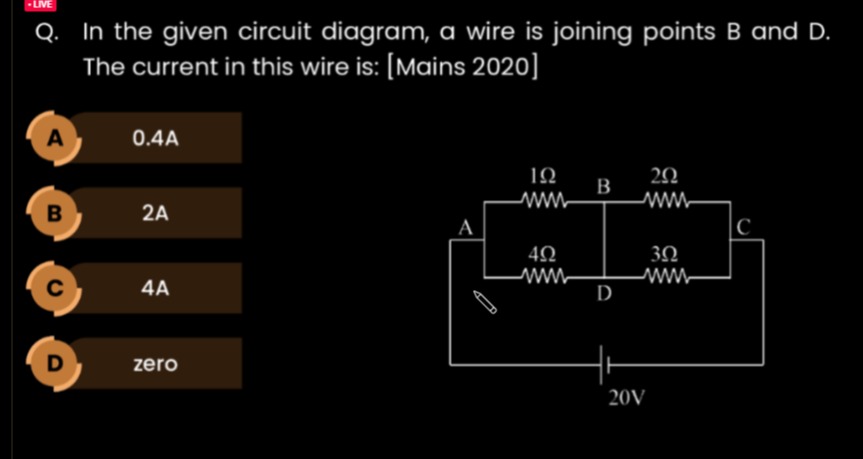
In the given circuit diagram, a wire is joining points B and D. The current in this wire is:
0.4A
2A
4A
zero
2A
Solution
The given circuit is a Wheatstone bridge with a 20V battery connected across points A and C, and a wire connecting points B and D. The resistances are RAB=1Ω, RBC=2Ω, RAD=4Ω, and RDC=3Ω. We need to find the current in the wire joining B and D.
Let VA, VB, VC, and VD be the potentials at points A, B, C, and D respectively. Let's set VC=0V and VA=20V since the battery is connected between A and C with the positive terminal at A.
Let IBD be the current flowing from B to D through the wire. We can use nodal analysis at points B and D.
At node B, by Kirchhoff's current law: Current entering B = Current leaving B IAB=IBC+IBD RABVA−VB=RBCVB−VC+IBD 120−VB=2VB−0+IBD 2(20−VB)=VB+2IBD 40−2VB=VB+2IBD 40=3VB+2IBD (Equation 1)
At node D, by Kirchhoff's current law: Current entering D = Current leaving D IAD+IBD=IDC RADVA−VD+IBD=RDCVD−VC 420−VD+IBD=3VD−0 3(20−VD)+12IBD=4VD 60−3VD+12IBD=4VD 60=7VD−12IBD (Equation 2)
The problem statement does not specify the resistance of the wire joining B and D. In such problems, it is usually assumed that the wire is ideal, meaning it has zero resistance. If the wire has zero resistance, then points B and D are at the same potential, i.e., VB=VD. Let VB=VD=V.
Substituting VB=V and VD=V into Equations 1 and 2: 40=3V+2IBD (Equation 3) 60=7V−12IBD (Equation 4)
We have a system of two linear equations with two unknowns, V and IBD. We can solve for IBD. Multiply Equation 3 by 7 and Equation 4 by 3: 7×(40=3V+2IBD)⟹280=21V+14IBD 3×(60=7V−12IBD)⟹180=21V−36IBD
Subtract the second new equation from the first new equation: (280)−(180)=(21V+14IBD)−(21V−36IBD) 100=14IBD+36IBD 100=50IBD IBD=50100=2A
The current in the wire joining B and D is 2A. Since we assumed the current flows from B to D and got a positive value, the direction of the current is from B to D.
We can also find the potential V: From Equation 3: 40=3V+2(2)⟹40=3V+4⟹3V=36⟹V=12V. So, VB=VD=12V.
