Question

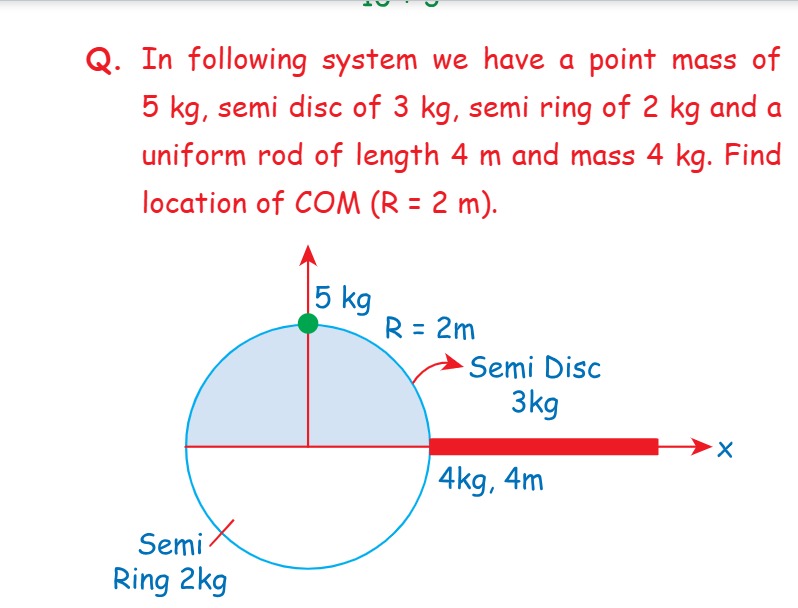
In following system we have a point mass of 5 kg, semi disc of 3 kg, semi ring of 2 kg and a uniform rod of length 4 m and mass 4 kg. Find location of COM (R = 2 m).

Answer 1

The location of the Center of Mass (COM) is $(\frac{4}{7}, \frac{5}{7})$ meters.

Answer 2

1. Point mass (5 kg): COM at (0, 2) m.
2. Semi-disc (3 kg, R=2m, upper half): COM at (0, $\frac{4R}{3\pi}$) = (0, $\frac{8}{3\pi}$) m.
3. Semi-ring (2 kg, R=2m, lower half): COM at (0, $-\frac{2R}{\pi}$) = (0, $-\frac{4}{\pi}$) m.
4. Uniform rod (4 kg, L=4m): COM at ($\frac{L}{2}$, 0) = (2, 0) m.

Total mass $M = 5 + 3 + 2 + 4 = 14$ kg.

$X_{COM} = \frac{5(0) + 3(0) + 2(0) + 4(2)}{14} = \frac{8}{14} = \frac{4}{7}$ m. $Y_{COM} = \frac{5(2) + 3(\frac{8}{3\pi}) + 2(-\frac{4}{\pi}) + 4(0)}{14} = \frac{10 + \frac{8}{\pi} - \frac{8}{\pi}}{14} = \frac{10}{14} = \frac{5}{7}$ m.