Question

In cylindrical shell $\rho_{(x)} = \frac{c}{x}$. Find $I$, $I_{(x)}$ and $E_{(x)} = ?$

Answer 1

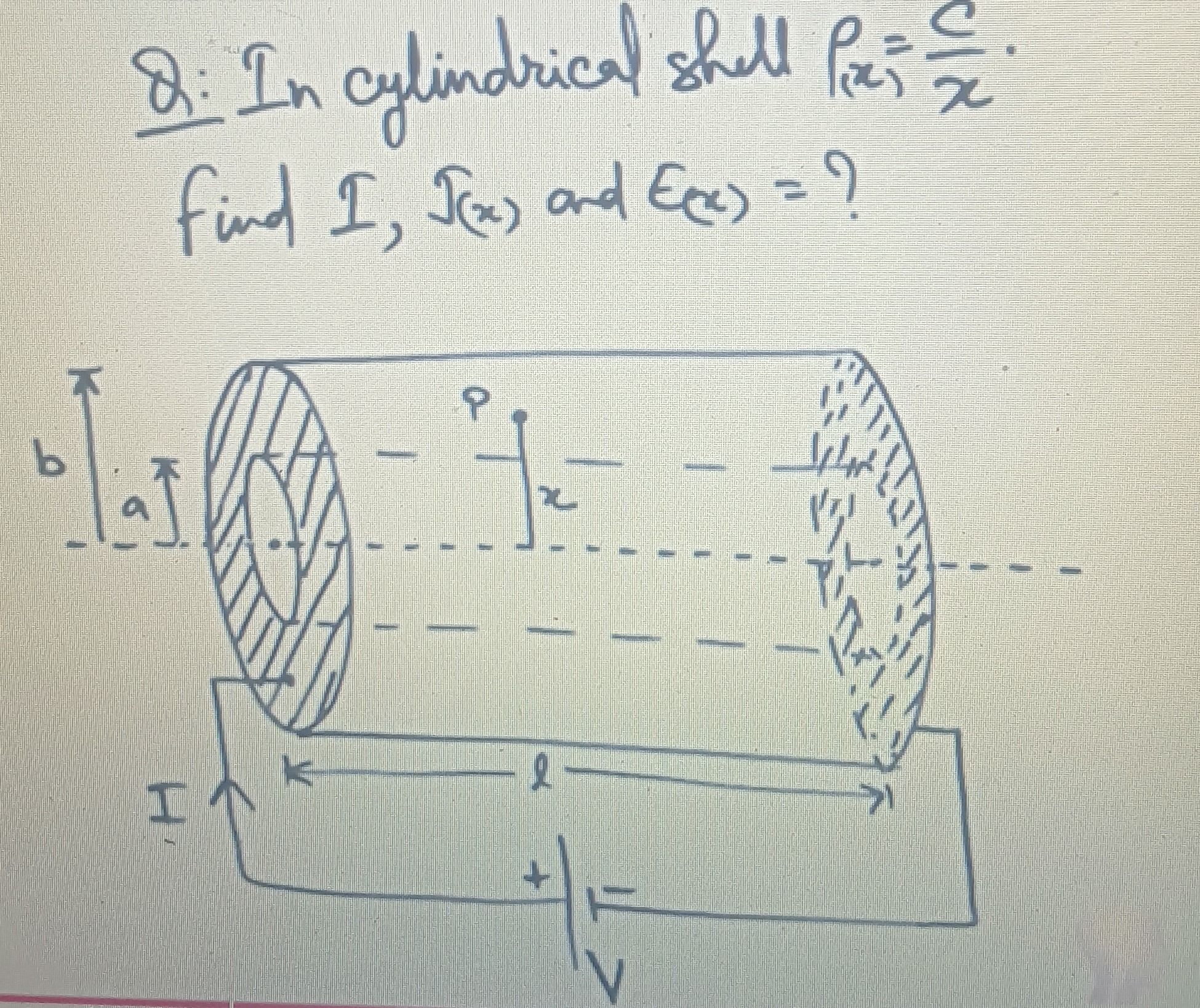
E(x) = V/l, J(x) = Vx/lc, I = (2πV/(3lc))(b^3-a^3), I(x) = (2πV/(3lc))(x^3-a^3)

Answer 2

The problem asks us to find the electric field $E(x)$, current density $J(x)$, total current $I$, and current $I(x)$ (cumulative current from inner radius $a$ to radius $x$) in a cylindrical shell.

1. Electric Field $E(x)$ The voltage $V$ is applied across the length $l$ of the cylindrical shell. Since the electric field lines are parallel to the axis of the cylinder and the potential difference is constant along the length, the electric field $E$ inside the conductor is uniform along its length and across its cross-section. Therefore, the electric field is given by: $E(x) = E = \frac{V}{l}$ This electric field is independent of the radial position $x$.

2. Current Density $J(x)$ According to Ohm's law in differential form, the current density $\vec{J}$ is related to the electric field $\vec{E}$ and resistivity $\rho$ by $\vec{E} = \rho \vec{J}$, or $J = E/\rho$. Given $\rho(x) = \frac{c}{x}$ and $E(x) = \frac{V}{l}$. Substituting these values: $J(x) = \frac{E(x)}{\rho(x)} = \frac{V/l}{c/x} = \frac{Vx}{lc}$ The current density $J(x)$ varies linearly with the radial distance $x$.

3. Total Current $I$ The total current $I$ flowing through the cylindrical shell is the integral of the current density $J(x)$ over its entire cross-sectional area. The cross-section is an annulus with inner radius $a$ and outer radius $b$. Consider an elementary annular ring of radius $x$ and thickness $dx$. The area of this elementary ring is $dA = 2\pi x dx$. The elementary current $dI$ through this ring is $dI = J(x) dA$. $dI = \left(\frac{Vx}{lc}\right) (2\pi x dx) = \frac{2\pi V}{lc} x^2 dx$ To find the total current $I$, integrate $dI$ from the inner radius $a$ to the outer radius $b$: $I = \int_{a}^{b} \frac{2\pi V}{lc} x^2 dx$ $I = \frac{2\pi V}{lc} \int_{a}^{b} x^2 dx = \frac{2\pi V}{lc} \left[ \frac{x^3}{3} \right]_{a}^{b}$ $I = \frac{2\pi V}{3lc} (b^3 - a^3)$

4. Current $I(x)$ Assuming $I(x)$ represents the cumulative current flowing through the cylindrical shell from the inner radius $a$ up to an arbitrary radial distance $x$ (where $a \le x \le b$). We integrate the elementary current $dI$ from $a$ to $x$: $I(x) = \int_{a}^{x} \frac{2\pi V}{lc} (x')^2 dx'$ $I(x) = \frac{2\pi V}{lc} \left[ \frac{(x')^3}{3} \right]_{a}^{x}$ $I(x) = \frac{2\pi V}{3lc} (x^3 - a^3)$ Note that for $x=b$, $I(b)$ gives the total current $I$.

Summary of Results:

• Electric Field: $E(x) = \frac{V}{l}$
• Current Density: $J(x) = \frac{Vx}{lc}$
• Total Current: $I = \frac{2\pi V}{3lc} (b^3 - a^3)$
• Cumulative Current (from $a$ to $x$): $I(x) = \frac{2\pi V}{3lc} (x^3 - a^3)$

The question is of descriptive type as it asks for multiple values and their expressions.