Question

If $x_{n+1} = (3 + \frac{2}{n} + \frac{1}{n^2} + \frac{\ln n}{n^3})x_n$ for all $n \in N$ and $x_1 = 4$

Evaluate $\lim_{n \to \infty} (x_n)^{\frac{1}{n}}$

Answer 1

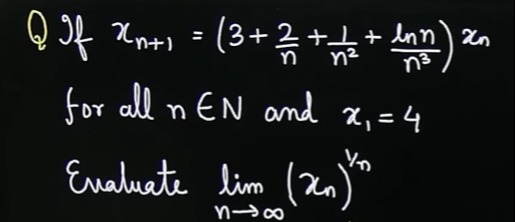
3

Answer 2

We are given the recurrence relation $x_{n+1} = (3 + \frac{2}{n} + \frac{1}{n^2} + \frac{\ln n}{n^3})x_n$ and $x_1 = 4$. We need to find $\lim_{n \to \infty} (x_n)^{\frac{1}{n}}$.

A key theorem states that if $\lim_{n \to \infty} \frac{x_{n+1}}{x_n} = L$, then $\lim_{n \to \infty} (x_n)^{\frac{1}{n}} = L$, provided $x_n > 0$ for all $n$.

First, we find the limit of the ratio $\frac{x_{n+1}}{x_n}$: $\frac{x_{n+1}}{x_n} = 3 + \frac{2}{n} + \frac{1}{n^2} + \frac{\ln n}{n^3}$

Now, we evaluate the limit of this ratio as $n \to \infty$: $\lim_{n \to \infty} \frac{x_{n+1}}{x_n} = \lim_{n \to \infty} \left(3 + \frac{2}{n} + \frac{1}{n^2} + \frac{\ln n}{n^3}\right)$ We evaluate each term separately: $\lim_{n \to \infty} 3 = 3$ $\lim_{n \to \infty} \frac{2}{n} = 0$ $\lim_{n \to \infty} \frac{1}{n^2} = 0$ For the term $\lim_{n \to \infty} \frac{\ln n}{n^3}$, we use L'Hopital's Rule as it is of the indeterminate form $\frac{\infty}{\infty}$: $\lim_{n \to \infty} \frac{\ln n}{n^3} = \lim_{n \to \infty} \frac{\frac{d}{dn}(\ln n)}{\frac{d}{dn}(n^3)} = \lim_{n \to \infty} \frac{1/n}{3n^2} = \lim_{n \to \infty} \frac{1}{3n^3} = 0$ Combining these limits, we get: $\lim_{n \to \infty} \frac{x_{n+1}}{x_n} = 3 + 0 + 0 + 0 = 3$ Since $x_1 = 4 > 0$, and the factor $(3 + \frac{2}{n} + \frac{1}{n^2} + \frac{\ln n}{n^3})$ is positive for all $n \in N$ (as $n \ge 1$, $3 + \frac{2}{n} + \frac{1}{n^2} > 0$, and $\frac{\ln n}{n^3} \ge 0$), it follows that $x_n > 0$ for all $n$. Therefore, applying the theorem: $\lim_{n \to \infty} (x_n)^{\frac{1}{n}} = \lim_{n \to \infty} \frac{x_{n+1}}{x_n} = 3$