Solveeit Logo
Login

Question

Question: If $x=1+3^{1/3}+9^{1/3}$ then value of $x^3-3x^2-6x$ is equal to...

If x=1+31/3+91/3x=1+3^{1/3}+9^{1/3} then value of x3−3x2−6xx^3-3x^2-6x is equal to

A

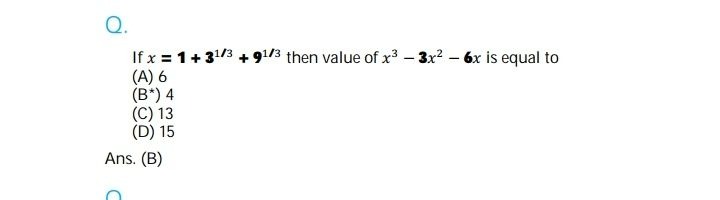
6

B

4

C

13

D

15

Answer

4

Explanation

Solution

Given the equation x=1+31/3+91/3x = 1 + 3^{1/3} + 9^{1/3}. We can rewrite 91/39^{1/3} as (32)1/3=32/3(3^2)^{1/3} = 3^{2/3}. So, the equation is x=1+31/3+32/3x = 1 + 3^{1/3} + 3^{2/3}. Rearrange the equation to isolate the terms with fractional exponents: x−1=31/3+32/3x - 1 = 3^{1/3} + 3^{2/3}.

Cube both sides of this equation: (x−1)3=(31/3+32/3)3(x - 1)^3 = (3^{1/3} + 3^{2/3})^3.

Expand the left side using the formula (a−b)3=a3−3a2b+3ab2−b3(a-b)^3 = a^3 - 3a^2b + 3ab^2 - b^3: (x−1)3=x3−3x2(1)+3x(1)2−13=x3−3x2+3x−1(x - 1)^3 = x^3 - 3x^2(1) + 3x(1)^2 - 1^3 = x^3 - 3x^2 + 3x - 1.

Expand the right side using the formula (a+b)3=a3+b3+3ab(a+b)(a+b)^3 = a^3 + b^3 + 3ab(a+b). Let a=31/3a = 3^{1/3} and b=32/3b = 3^{2/3}. (31/3+32/3)3=(31/3)3+(32/3)3+3(31/3)(32/3)(31/3+32/3)(3^{1/3} + 3^{2/3})^3 = (3^{1/3})^3 + (3^{2/3})^3 + 3(3^{1/3})(3^{2/3})(3^{1/3} + 3^{2/3}). Calculate the terms: (31/3)3=3(3^{1/3})^3 = 3. (32/3)3=32=9(3^{2/3})^3 = 3^2 = 9. 31/3⋅32/3=31/3+2/3=33/3=31=33^{1/3} \cdot 3^{2/3} = 3^{1/3 + 2/3} = 3^{3/3} = 3^1 = 3. From the rearranged equation, 31/3+32/3=x−13^{1/3} + 3^{2/3} = x - 1.

Substitute these values back into the expansion of the right side: (31/3+32/3)3=3+9+3(3)(x−1)=12+9(x−1)=12+9x−9=3+9x(3^{1/3} + 3^{2/3})^3 = 3 + 9 + 3(3)(x - 1) = 12 + 9(x - 1) = 12 + 9x - 9 = 3 + 9x.

Now, equate the expanded left and right sides: x3−3x2+3x−1=3+9xx^3 - 3x^2 + 3x - 1 = 3 + 9x.

We need to find the value of x3−3x2−6xx^3 - 3x^2 - 6x. Rearrange the equation obtained to match this expression: x3−3x2+3x−9x−1=3  ⟹  x3−3x2−6x−1=3x^3 - 3x^2 + 3x - 9x - 1 = 3 \implies x^3 - 3x^2 - 6x - 1 = 3. Add 1 to both sides: x3−3x2−6x=3+1  ⟹  x3−3x2−6x=4x^3 - 3x^2 - 6x = 3 + 1 \implies x^3 - 3x^2 - 6x = 4.

The value of x3−3x2−6xx^3 - 3x^2 - 6x is 4.