Solveeit Logo
Login

Question

Question: If \(P = \begin{bmatrix} 1 & \alpha & 3 \\[6pt] 1 & 3 & 3 \\[6pt] 2 & 4 & 4 \end{bmatrix}\) is the a...

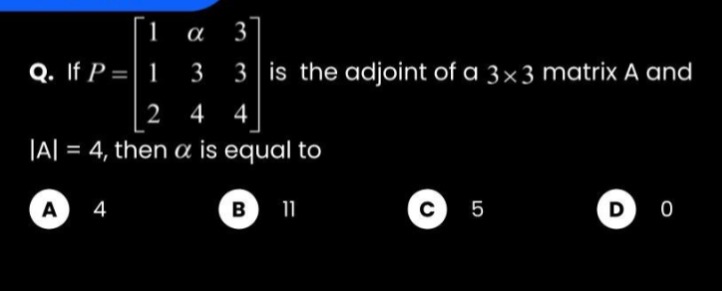
If P=[1α3133244]P = \begin{bmatrix} 1 & \alpha & 3 \\[6pt] 1 & 3 & 3 \\[6pt] 2 & 4 & 4 \end{bmatrix} is the adjoint of a 3×3 matrix AA and ∣A∣=4\lvert A\rvert = 4, then α\alpha is equal to

A

4

B

11

C

5

D

0

Answer

11

Explanation

Solution

Key steps:

  1. Property of adjoint:

    det⁡(\adj(A))  =  (det⁡A)n−1for an n×n matrix.\det\bigl(\adj(A)\bigr) \;=\;\bigl(\det A\bigr)^{n-1} \quad\text{for an }n\times n\text{ matrix.}

    Here n=3n=3 and det⁡A=4\det A = 4, so

    det⁡(P)  =  det⁡(\adj(A))  =  4 3−1  =  16.\det(P) \;=\; \det\bigl(\adj(A)\bigr) \;=\;4^{\,3-1} \;=\;16.

  2. Compute det⁡(P)\det(P) in terms of α\alpha:

    det⁡ ⁣P=1∣3344∣−α∣1324∣+3∣1324∣=0  −  α(4−6)  +  3(4−6)=2α  −  6.\det\!P = 1 \begin{vmatrix}3 & 3\\[3pt]4 & 4\end{vmatrix} -\alpha \begin{vmatrix}1 & 3\\[3pt]2 & 4\end{vmatrix} +3 \begin{vmatrix}1 & 3\\[3pt]2 & 4\end{vmatrix} = 0 \;-\;\alpha(4-6)\;+\;3(4-6) = 2\alpha \;-\;6.

  3. Set equal to 16:

    2α−6=16⟹2α=22⟹α=11.2\alpha - 6 = 16 \quad\Longrightarrow\quad 2\alpha = 22 \quad\Longrightarrow\quad \alpha = 11.