Question
Question: If matrix A is \[ \begin{bmatrix} 1 & -1 & 2 \\ 3 & 0 & -2 \\ 1 & 0 & 3 \end{bmatrix}, \] then valu...
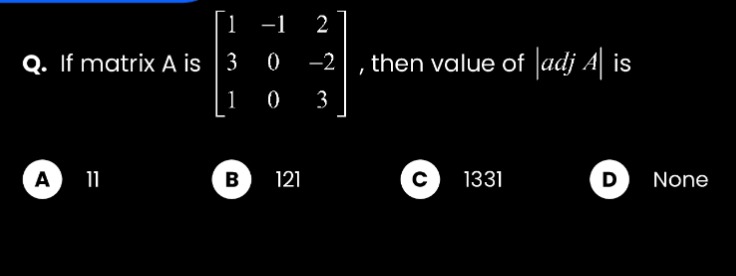
If matrix A is
131−1002−23,then value of ∣adjA∣ is
A
11
B
121
C
1331
D
None
Answer
121
Explanation
Solution
Step 1: Compute detA.
detA=1(0⋅3−(−2)⋅0)−(−1)(3⋅3−(−2)⋅1)+2(3⋅0−0⋅1)=0+1⋅(9+2)+0=11.Step 2: Use the property
For an n×n matrix A,
Here n=3, so
∣adjA∣=(detA)2=112=121.