Question
Question: If inverse of \(A = \begin{bmatrix} \alpha & 1 & 2 \\[6pt] 0 & 3 & 1 \\[6pt] 1 & 1 & 1 \end{bmatrix}...
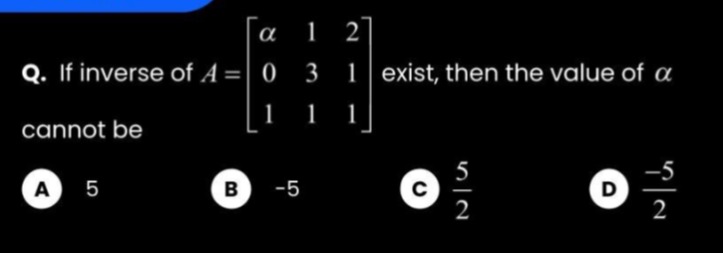
If inverse of A=α01131211 exist, then the value of α cannot be
A
5
B
-5
C
25
D
2−5
Answer
25
Explanation
Solution
To have an inverse, det(A)=0. Compute the determinant by cofactor expansion along the first row:
det(A)=α3111−10111+20131.Evaluate each minor:
3111=3⋅1−1⋅1=2,0111=0⋅1−1⋅1=−1,0131=0⋅1−3⋅1=−3.Thus,
det(A)=α⋅2−1⋅(−1)+2⋅(−3)=2α+1−6=2α−5.For det(A)=0, we require 2α−5=0, i.e.\ α=25.
