Question
Question: If $\int \frac{(2x^2+1)}{(x^2-4)(x^2-1)} = log\left[\left(\frac{x+1}{x-1}\right)^a \left(\frac{x-2}{...
If ∫(x2−4)(x2−1)(2x2+1)=log[(x−1x+1)a(x+2x−2)b]+c
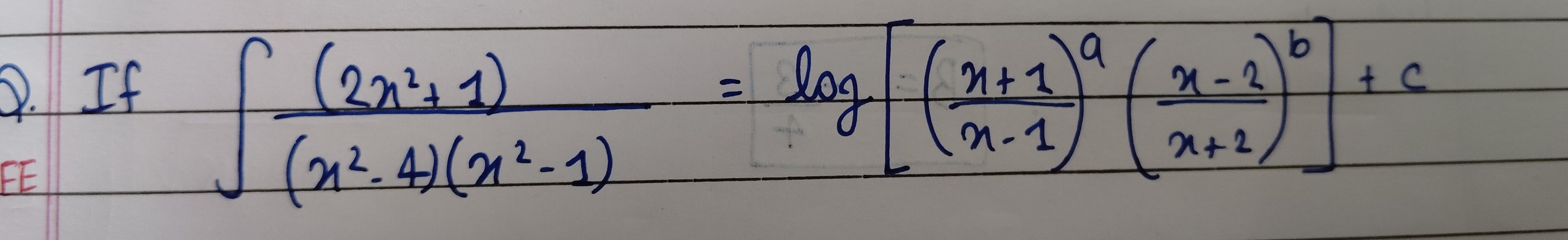
a=1/2, b=3/4
Solution
The problem requires us to evaluate the given integral and then compare it with the provided logarithmic form to find the values of 'a' and 'b'.
1. Partial Fraction Decomposition: The integrand is (x2−4)(x2−1)2x2+1. Let y=x2. Then the expression becomes (y−4)(y−1)2y+1. We can decompose this into partial fractions: (y−4)(y−1)2y+1=y−4A+y−1B Multiply both sides by (y−4)(y−1): 2y+1=A(y−1)+B(y−4) To find A, set y=4: 2(4)+1=A(4−1)⟹9=3A⟹A=3 To find B, set y=1: 2(1)+1=B(1−4)⟹3=−3B⟹B=−1 Substitute A and B back into the partial fraction form, and then replace y with x2: (x2−4)(x2−1)2x2+1=x2−43−x2−11
2. Integration: Now, integrate each term: ∫(x2−4)(x2−1)(2x2+1)dx=∫(x2−43−x2−11)dx =3∫x2−221dx−∫x2−121dx Using the standard integral formula ∫x2−a21dx=2a1logx+ax−a+C: For the first term, a=2: 3∫x2−221dx=3(2⋅21logx+2x−2)=43logx+2x−2 For the second term, a=1: −∫x2−121dx=−(2⋅11logx+1x−1)=−21logx+1x−1 Combining these results, the integral is: I=43logx+2x−2−21logx+1x−1+C
3. Manipulate to Match the Given Form: The given form is log[(x−1x+1)a(x+2x−2)b]+c. We need to transform our result to match this form. Using the logarithm property log(NM)=−log(MN), we can rewrite the second term: −21logx+1x−1=−21(−logx−1x+1)=21logx−1x+1 So the integral becomes: I=43logx+2x−2+21logx−1x+1+C Rearranging the terms to match the order in the question: I=21logx−1x+1+43logx+2x−2+C Now, use the logarithm property klogM=logMk: I=log(x−1x+1)1/2+log(x+2x−2)3/4+C Finally, use the logarithm property logM+logN=log(MN): I=log[(x−1x+1)1/2(x+2x−2)3/4]+C
4. Compare Exponents: Comparing this result with the given form log[(x−1x+1)a(x+2x−2)b]+c: We can directly identify the values of 'a' and 'b': a=21 b=43
