Question

If acdⁿ of Particle is given by eqⁿ $\overrightarrow{a}$ = (2x+1) m/s², where x is in mater (m). If at x=1m, v=2m/sec. Then find v as f(x) (Junction of position)

$\overrightarrow{a}$ = $\int 2x+1$

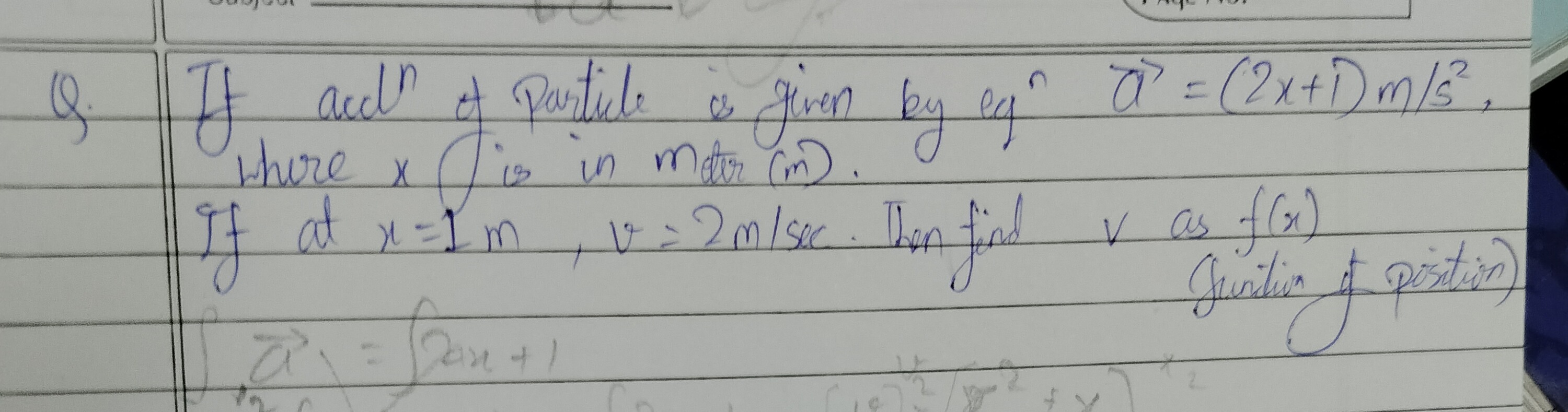
Answer 1

$v(x) = \sqrt{2x^2 + 2x}$

Answer 2

The acceleration $a$ is given as a function of position $x$. The relationship between $a$, $v$, and $x$ is $a = v \frac{dv}{dx}$. Substitute $a = 2x+1$ into this equation: $v \frac{dv}{dx} = 2x+1$. Separate the variables to get $v \, dv = (2x+1) \, dx$. Integrate both sides: $\int v \, dv = \int (2x+1) \, dx$, which yields $\frac{v^2}{2} = x^2 + x + C$. Use the initial condition $v=2$ at $x=1$ to find the integration constant $C$: $\frac{2^2}{2} = 1^2 + 1 + C \implies 2 = 2 + C \implies C=0$. Substitute $C=0$ back into the equation: $\frac{v^2}{2} = x^2 + x$. Solve for $v$: $v^2 = 2x^2 + 2x$, so $v = \pm \sqrt{2x^2 + 2x}$. Given the initial condition $v=2$ (positive) at $x=1$, we choose the positive root, $v(x) = \sqrt{2x^2 + 2x}$.