Solveeit Logo
Login

Question

Question: If a non-singular matrix A satisfies the equation $A^2-6A+17I=O$, then $A^{-1}$ is equal to :...

If a non-singular matrix A satisfies the equation A2−6A+17I=OA^2-6A+17I=O, then A−1A^{-1} is equal to :

A

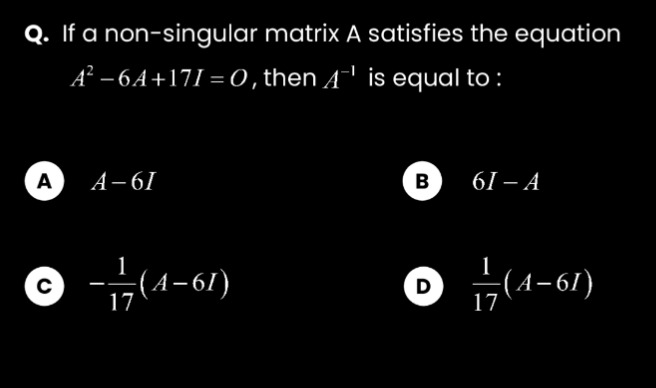
A-6I

B

6I-A

C

-\frac{1}{17}(A-6I)

D

\frac{1}{17}(A-6I)

Answer

-\frac{1}{17}(A-6I)

Explanation

Solution

Given the matrix equation A2−6A+17I=OA^2 - 6A + 17I = O. Since A is a non-singular matrix, its inverse A−1A^{-1} exists. We can multiply the given equation by A−1A^{-1} from the left:

A−1(A2−6A+17I)=A−1OA^{-1}(A^2 - 6A + 17I) = A^{-1}O

Using the distributive property of matrix multiplication:

A−1A2−A−1(6A)+A−1(17I)=OA^{-1}A^2 - A^{-1}(6A) + A^{-1}(17I) = O

Using the properties of matrix multiplication (AB)C=A(BC)(AB)C = A(BC) and scalar multiplication (kA)B=k(AB)(kA)B = k(AB):

(A−1A)A−6(A−1A)+17(A−1I)=O(A^{-1}A)A - 6(A^{-1}A) + 17(A^{-1}I) = O

Using the properties of inverse matrix A−1A=IA^{-1}A = I and identity matrix IA=AIA = A, IX=XIX = X:

IA−6I+17A−1=OIA - 6I + 17A^{-1} = O

A−6I+17A−1=OA - 6I + 17A^{-1} = O

Now, we want to isolate A−1A^{-1}. Rearrange the terms:

17A−1=O−A+6I17A^{-1} = O - A + 6I

17A−1=6I−A17A^{-1} = 6I - A

Divide by 17:

A−1=117(6I−A)A^{-1} = \frac{1}{17}(6I - A)

We can rewrite this expression as:

A−1=117(6I−A)=117(−A+6I)=−117(A−6I)A^{-1} = \frac{1}{17}(6I - A) = \frac{1}{17}(-A + 6I) = -\frac{1}{17}(A - 6I)