Question

If $2f(x)-3f(\frac{1}{x})=x^2, x$ is not equal to zero, then $f(2)$ is equal to

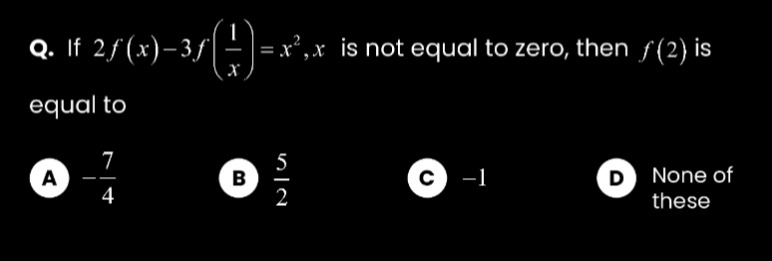
• A. $-\frac{7}{4}$
• B. $\frac{5}{2}$
• C. -1
• D. None of these

Answer 1

Answer: (A)

-\frac{7}{4}

Answer 2

To find $f(2)$, we substitute $x=2$ into the given equation: $2f(2) - 3f\left(\frac{1}{2}\right) = 4$

Next, substitute $x = \frac{1}{2}$ into the original equation: $2f\left(\frac{1}{2}\right) - 3f(2) = \frac{1}{4}$

Now we have a system of two equations:

1. $2f(2) - 3f\left(\frac{1}{2}\right) = 4$
2. $2f\left(\frac{1}{2}\right) - 3f(2) = \frac{1}{4}$

Multiply the first equation by 2 and the second equation by 3:

1. $4f(2) - 6f\left(\frac{1}{2}\right) = 8$
2. $6f\left(\frac{1}{2}\right) - 9f(2) = \frac{3}{4}$

Add the two equations to eliminate $f\left(\frac{1}{2}\right)$: $-5f(2) = 8 + \frac{3}{4} = \frac{32}{4} + \frac{3}{4} = \frac{35}{4}$

Solve for $f(2)$: $f(2) = -\frac{35}{4 \cdot 5} = -\frac{7}{4}$

Therefore, $f(2) = -\frac{7}{4}$.